Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas fundamentais - Ex. 9
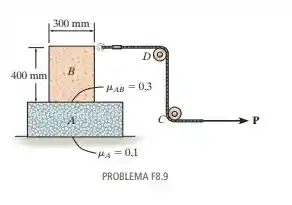
Os blocos A e B têm massas de e , respectivamente. Usando os coeficientes de atrito estático indicados, determine a maior força P que pode ser aplicada à corda sem causar movimento. Há polias em C e D.
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Partiu mais uma questão de Resmat.
Primeiramente, a força normal que sustenta os blocos é dada por:
Portanto, a força de atrito será:
Portanto:
Prontinho, esta é a força máxima que pode ser aplicada.
Resposta
Exercícios de Livros Relacionados
Se θ = 30 ° , determine o menor coeficiente de atrito estático em A e B de modo que o equilíbrio da estrutura de suporte seja mantido, independentemente da massa do cilindro. Desconsidere a massa das
Determine a força horizontal P máxima que pode ser aplicada à argola de 12k g sem fazer com que ela gire. O coeficiente de atrito estático entre a argola e as superfícies em A e B é μ s = 0,2 . Consid
Se o coeficiente de atrito estático em A e B é μ s = 0,6 , determine o ângulo máximo θ para o sistema permanecer em equilíbrio, independentemente da massa do cilindro. Desconsidere a massa das hastes.
O disco de 100k g se apoia em uma superfície para a qual μ B = 0,2 . Determine a menor força vertical P que pode ser aplicada tangencialmente ao disco que causará o movimento iminente.
A argola uniforme de peso W está sujeita à força horizontal P . Determine o coeficiente de atrito estático entre a argola e as superfícies em A e B se a argola estiver na iminência de rotação.