Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 28
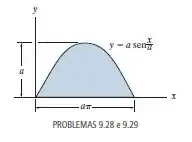
Localize o centroide da área.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Sabemos que o ângulo de fricção é dado por:
Portanto:
O ângulo de avanço do parafuso é dado por:
Substituindo os dados, temos que:
Passo 2
Agora vamos calcular o menor torque necessário para afrouxar o parafuso. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
Localiza o centroide z - do sólido homogêneo formado girando-se a área sombreada em torno do eixo y .
Localize o centroide y - do sólido homogêneo formado girando-se a área sombreada em torno do eixo y .
Localize o centroide z - do frustum sólido homogêneo do paraboloide formada girando-se a área sombreada em torno do eixo z .
Determine a massa e a localização do centro de massa y - do hemisfério formado girando-se a área sombreada em torno do eixo y . A densidade em qualquer ponto no hemisfério pode ser definida por ρ = ρ
Se a densidade em qualquer ponto na placa retangular é definida por ρ = ρ 0 1 + x a , onde ρ 0 é uma constante, determine a massa e localize o centro de massa x - da placa. A placa tem uma espessura t