Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 37

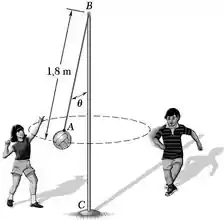
Uma bola presa a uma corda se move ao longo de uma trajetória circular a uma velocidade escalar constante de 4 m/s. Determine (a) o ângulo θ que a corda forma com o poste BC, (b) a tração na corda.

Passo 1

Partiu mais um exercício de resmat, vamos determinar (a) a aceleração de B relativa a A, (b) a tração no cabo CD.

Primeiro consideramos que as acelerações são dadas por:

a A = a n = v A 2 ρ

Passo 2

  1. + ↑ Σ F y = 0 :       T B C sin ⁡ 60 ° - W A = 0

    ou

    T A B = m A g cos ⁡ θ

    → + Σ F x = m A a A :         T A B sin ⁡ θ = m A v A 2 ρ

    Substituindo TAB e ρ

    m A g cos ⁡ θ sin ⁡ θ = m A v A 2 l A B sin ⁡ θ

    sin 2 θ = 1 - cos 2 θ

    1 - c o s 2 θ = 4   m/ m 2 1.8   m × 9.81   m/ s 2 cos ⁡ θ

    ou

    cos 2 θ + 0.906105 cos ⁡ θ - 1 = 0

    Resolvendo

    cos ⁡ θ = 0.64479

    Passo 2

  2. De cima

T A B = m A g cos ⁡ θ = 0.450   kg × 9.81   m/ s 2 0.64479

Resposta

a )   θ = 49.9 °

b)  T A B = 6.85   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco A tem massa de 2k g e desliza para dentro de uma caixa com as extremidades abertas a uma velocidade de 2m / s . Se a caixa B tem massa de 3k g e está em repouso sobre a placa P , que tem massa
O bloco A tem massa de 2k g e desliza para dentro de uma caixa B com as extremidades abertas a uma velocidade de 2m / s . Se a caixa B tem massa de 3k g e está em repouso sobre a placa P , que tem mas
Se o homem de 75k g dispara a bala de 0 , 1k g , a uma velocidade de saída horizontal de 900m / s , medida relativamente ao carrinho de 300k g , determine a velocidade do carrinho logo após o disparo.
No Problema 15.61 determine a força resultante média entre os blocos A e B durante o impacto, se este ocorre em 0,005 segundos.
Uma bola de 1k g está viajando horizontalmente a 20m / s quando atinge um bloco B de 10k g que está em repouso. Se o coeficiente de restituição entre A eB é e = 0,6 e o coeficiente de atrito cinético