O bloco A tem massa de 10 kg e os blocos B e C de 5 kg cada. Sabendo que os blocos estão inicialmente em repouso e que B percorre uma distância de 2,4 m em 2 s, determine (a) a intensidade da força P, (b) a tração na corda AD. Despreze as massas das roldanas e o atrito no eixo.

Passo 1
Vamos posicionar a coordenada y como positiva e para baixo. Vejam o esboço que utilizaremos para determinarmos a questão
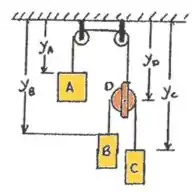
Limite da corda AD:
Limite de corda BC:
Eliminando .
(1)
Passo 2
Nós aceleramos o movimento uniformemente por causa de todas as forças serem constantes.
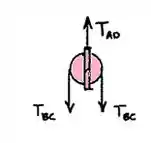
Polia D:
Passo 3
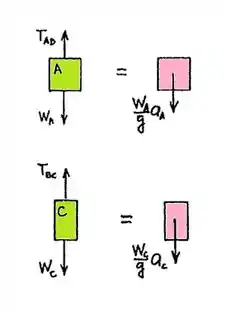
(2)
(3)
Passo 4
Substituindo o valor por e as Eqs. (2) e (3) na Eq. (1), e resolvendo para ,
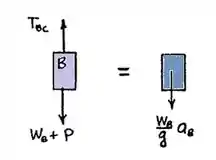
Bloco B:
Passo 5
(a)Magnitude de P.
(b)Tensão na corda AD.