Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 43

O bloco A tem massa de 2   k g e desliza para dentro de uma caixa com as extremidades abertas a uma velocidade de 2   m / s . Se a caixa B tem massa de 3   k g e está em repouso sobre a placa P , que tem massa de 3   k g , determine a distância que a placa percorre depois que parar de deslizar sobre o solo. Além disso, quanto tempo se passa depois do impacto antes que cesse todo o movimento? O coeficiente de atrito cinético entre a caixa e a placa é μ k = 0,2 e entre a placa e o solo é μ ' k = 0,4 . E, ainda, o coeficiente de atrito estático entre a placa e o solo é μ ' s = 0,5 .

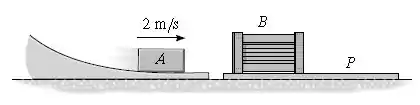
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O diagrama de corpo livre da caixa é dado por:

+ ↑ ∑ F y = 0

N B - 3 + 2 9,81 = 0

N B = 49,05   N

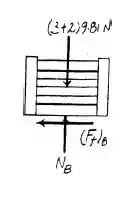
Quando a caixa B começa a deslizar sobre a placa, temos:

+ ↑ ∑ F y = 0

N P - 49,05 - 3 9,81 = 0

N P = 78,48   N

→ + ∑ F x = 0

9,81 - F f P = 0

F f P = 9,81   N

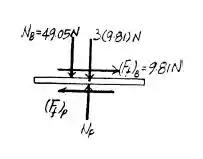
Se F f P < F f P m á x = μ s ' N P = 0,5 78,48 = 39,24   N , a placa não se move. Como F f P = 9,81   N , esta condição é respeitada.

s P = 0

Passo 2

Considerando o bloco e a caixa como um sistema podemos aplicar conservação de quantidade de movimento:

→ +         m A v A 1 + m R v R 1 = m A + m R v 2

Substituindo os valores, temos:

→ +         2 ( 2 ) + 0 = 2 + 3 v 2

v 2 = 0,8   m / s     ( → )

Aplicando o principio do impulso e quantidade de movimento, temos:

→ +         m v x 1 + ∑ ∫ t 1 t 2 F x d t = m v x 2

→ +       5 0,8 + - 9,81 t = 5 ( 0 )

t = 0,408   s

Resposta

s P = 0

t = 0,408   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em operação, o ventilador de jato de ar descarrega o ar a uma velocidade de v B = 20m / s para dentro de um bocal tendo um diâmetro de 0,5m . Se o ar tem uma densidade de 1,22k g / m 3 , determine as
A lâmina divide o jato de água que tem diâmetro de 75m m . Se um quarto da água flui para baixo, enquanto três quartos fluem para cima, e o fluxo total é Q = 0,0135m 3 / s , determine as componentes h
A pressão da água em C é 300k N / m 2 . Se a água flui para fora do cano em A e B , com velocidades v A = 3,6m / s e v B = 7,5m / s , determine as componentes da força horizontal e vertical exercidos
As rodas do carro de 1,5 Mg geram a força de tração F descrita pelo gráfico. Se o carro parte do repouso, determine a sua velocidade quando t = 6s.
Se o coeficiente de atrito cinético entre a caixa de 750N (m≈75 kg) e o solo é μ k = 0,2, determine a velocidade da caixa quando t=4s. A caixa parte do repouso e é arrastada pela força de 500 N.