Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 42
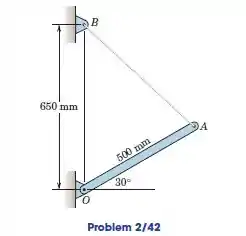
O cabo carrega uma tensão de . Determine o momento, em relação a , da tensão aplicada ao ponto da barra delgada.
Passo 1
E aí, tudo joinha?
Nesse problema precisamos determinar o momento, em relação a , da tensão aplicada ao ponto da barra. Vamos começar desenhando:
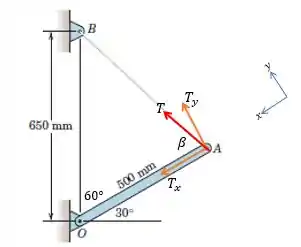
Veja que, adotamos um eixo , no qual o eixo é perpendicular a barra . Para obter o ângulo , temos que,
Nos foram dadas as seguintes informações:
Agora vamos aplicar a lei dos cossenos para encontrar a medida do segmento .
Aplicando a lei dos senos, encontramos o ângulo :
Passo 2
Estamos terminando! Urruh!
Observe que o momento de é zero.
Considerando o sentido anti-horário positivo:
no sentido anti-horário.
*veja que já substitui a distância convertida de para .
Resposta
Exercícios de Livros Relacionados
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Expresse F 1 , F 2 e F 3 como vetores cartesianos.
Determine as componentes x e y de cada força que atua sobre a chapa de fixação de uma treliça de ponte. Mostre que a força resultante é zero.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.