Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 121
Um cabo passa em torno de três tubos paralelos. Dois dos tubos são fixos e não podem rolar, enquanto o terceiro tubo é girado vagarosamente. Sabendo que os coeficientes de atrito são e , determine o maior peso que pode ser erguido se apenas o tubo está rodando no sentido anti-horário. se apenas o tubo está rodadno no sentido horário.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O primeiro a se fazer é determinar as reações do mecanismo apresentando através do seu diagrama de corpo livre:
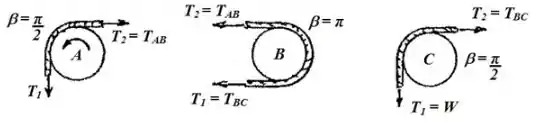
Para o tubo , obteremos relação entre as tensões e força peso :
Para o tubo , obteremos relação entre as tensões:
E para o tubo , obteremos relação entre as tensões e a força peso:
Passo 2
Teremos então a seguinte equação entre as reações e a força peso do sistema:
Passo 3
Para o item , temos que está girando no sentido horário:
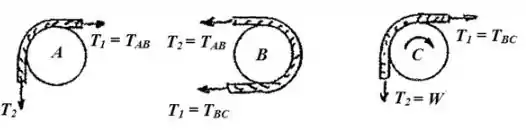
Para o tubo , obteremos relação entre as tensões e força peso :
Para o tubo , obteremos relação entre as tensões:
E para o tubo , obteremos relação entre as tensões e a força peso:
Passo 4
Teremos então a seguinte equação entre as reações e a força peso do sistema: