Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 134

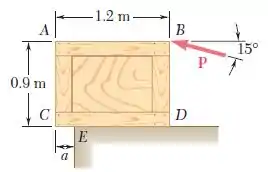
Um trabalhador move vagarosamente um caixote com 50   k g para a esquerda ao longo de uma plataforma de carga aplicando uma força P no canto B como mostra a figura. Sabendo que o caixote começa a inclinar-se sobre a extremidade E da plataforma de carga quando a = 200   m m , determine a o coeficiente de atrito cinético entre o caixote e a plataforma de carga, b a intensidade correspondente da força P .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos analisar o diagrama de corpo livre da caixa com a linha de ação da força e da reação:

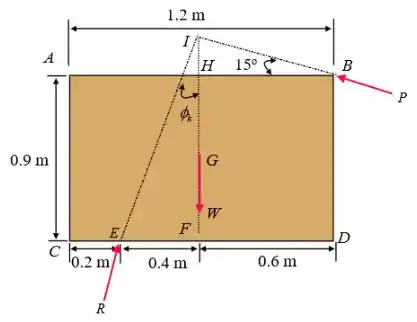
Vamos calcular o comprimento H I :

H I = F D ⋅ tan ⁡ 15 °

H I = 0,6 tan ⁡ 15 °

H I = 0,160769   m

Agora, vamos calcular F I :

F I = F H + H I

F I = 0,9 + 0,160769

F I = 1,060769   m

Passo 2

Podemos calcular o coeficiente de atrito cinético a partir da seguinte relação:

μ k = tan ⁡ ϕ k

μ k = E F F I

Sabendo que E F = 0,4   m e F I = 1,060769   m , temos que:

μ k = 0,37708

Passo 3

Vamos calcular o ângulo de atrito:

ϕ k = tan - 1 ⁡ μ k

ϕ k = 20,66 °

Agora vamos analisar o triângulo de força para a caixa:

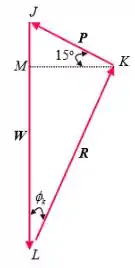
Temos que o ângulo K J M é dado por:

∠ K J M = 90 ° - 15 °

∠ K J M = 75 °

Portanto, o ângulo J K L é dado por:

∠ J K L = 180 ° - 75 ° - 20,66 °

∠ J K L = 84,34 °

Passo 4

Como descobrimos os ângulos, podemos aplicar a lei dos senos para encontrar P :

P sen ⁡ ϕ k = W sen ⁡ ∠ J K L

P = sen ⁡ 20,66 ° sen ⁡ 84,34 ° W

Como W = m g = 50 9,81 = 490,5   N , temos que:

P = 173,9   N

Resposta

P = 173,9   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a menor força P necessária para levantar a caixa de 40k g . O coeficiente de atrito estático entre o cabo e cada pino é μ s = 0,1 .
A viga lisa está sendo içada por meio de uma corda envolvendo a viga e passando por um anel em A , conforme mostrado. Se a extremidade da corda está sujeita a uma tração T e o coeficiente de atrito es
Uma correia em “ V ” é usada para conectar o eixo A do motor à roda B . Se a correia pode sustentar uma tração máxima de 1200N , determine a maior massa do cilindro C que pode ser levantada e o torque
O bloco A tem massa de 50k g e repousa sobre uma superfície para a qual μ s = 0,25 . Se o coeficiente de atrito estático entre a corda e o pino fixo em C é μ s ' = 0,3 , determine a maior massa do cil
O bloco A se apoia sobre a superfície para a qual μ s = 0,25 . Se a massa do cilindro suspenso D é 4k g , determine a menor massa do bloco A para que ele não deslize ou tombe. O coeficiente de atrito