Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 131
Resolva o Problema supondo que a correia plana e os tambores sejam substituídos por uma correia em e por polias em com . (O ângulo é mostrado na Fig. .)
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos o seguinte diagrama do tambor :
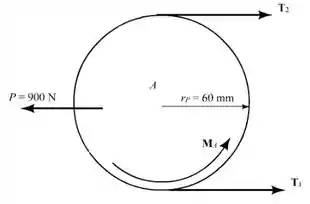
Aqui, temos que:
Passo 2
Considerando a relação para as tensões em um tambor, temos que:
Temos que:
Portanto:
E:
Passo 3
Aplicando a condição de equilíbrio do ponto , temos que:
Substituindo e resolvendo, temos que:
Resposta
Exercícios de Livros Relacionados
Uma enceradeira elétrica de 225N é operada sobre uma superficie cujo coeficiente de atrito cinético é 0,25 . Considerando que a força normal por unidade de área entre o disco e o assoalho é distríbuid
Uma alavanca A B de peso desprezivel é montada com folga em um eixo fixo de 63m m de diâmetro. Sabendo que o coeficiente de atrito estático entre o eixo fixo e a alavanca é 0,15 ; determine P necessár
Sabendo que é necessário um torque de intensidade 30N ⋅ m para iniciar a rotação do eixo vertical, determine o coeficiente de atrito estático entre as superficies anelares de contato.
Sabendo que o coeficiente de atrito estático é 0,30 e que o tambor de freio está rodando no sentido anti-horário, determine o mínimo valor de a para o qual o freio não é autotravante.
Um cabo passa em torno de três tubos paralelos. Dois dos tubos são fixos e não podem rodar, enquanto o terceiro tubo é girado vagarosamente. Sabendo que os coeficientes de atrito são μ s = 0,25 e μ k