Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 32

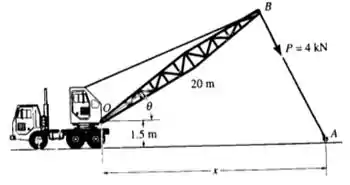
32. O cabo de reboque exerce uma força P = 4   k N na extremidade da lança do guindaste de 20 m de comprimento. Se θ = 30 ° , determine o posicionamento x do gancho em A para que essa força crie um momento máximo em relação ao ponto O. Qual é esse momento?

Passo 1

Primeiro uma coisa temos que ter em mente para o momento ser máximo, o ângulo entre OB e BA tem que ser 90°, então temos que ajeitar x de forma que isso aconteça.

Uma coisa que devemos fazer é descobrir o seguinte ângulo quando temos o de 90°.

O ângulo inferior (vamos chamar de ϕ ) que está marcado é o que queremos saber e que é igual ao superior.

Como queremos o caso OB perpendicular a BA, logo:

θ + 90 + ϕ = 180 °

Como θ = 30 ° :

30 ° + 90 + ϕ = 180 °

ϕ = 60 °

Assim para ter a condição que queríamos ϕ = 60 ° .

Passo 2

Considerando OB perpendicular a BA temos o que o momento é máximo como foi dito e logo:

M 0 = F d

M 0 = 4   k N ⋅ 20   m = 4000   k N ⋅ 20   m = 80000   N ⋅ m = 80   k N ⋅ m

Mas isso não conseguimos x daí.

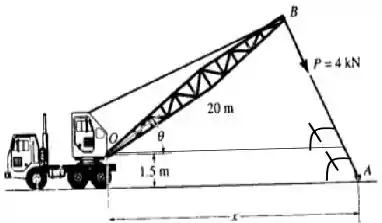
Para achar x devemos notar que como o eixo de rotação tem uma certa altura acima do chão então tanto a componente x tanto a componente y da força tem papeis no valor do momento.

Então o momento total no caso OB perpendicular a BA também pode ser calculado somando os momentos referentes a cada componente da força. Podemos chamar a força da componente x de P x = P cos ⁡ ϕ e a componente y de P y = P   s e n   ϕ . Pode ficar mais claro de ver isso na figura a seguir:

Então pelo princípio dos momentos podemos calcular o momento total, somando o momento em relação a P x que é P x vezes o seu braço de momento perpendicular a ele que aí no caso é 1,5 m com o momento em relação a P y que é P y vezes seu braço de momento perpendicular a ele que é x.

Um esclarecimento o braço de momento é a distância do eixo até o ponto de aplicação da força, nesse caso o braço de momento tem duas componentes, uma em x que vale x e uma em y que vale 1,5.

Passo 3

Vamos calcular o momento total mais uma vez, mas dessa nova forma.

Primeiro o mento de P x :

M 0 x = - P x ⋅ 1,5   m

O sinal representa que essa força faz o eixo rodar no sentido horário.

M 0 x = - 4   k N cos ⁡ 60 ° ⋅ 1,5   m

Agora o momento de P y :

M 0 y = P y ⋅ x   m

M 0 y = 4   k N   s e n   60 ° ⋅ x   m

Logo o momento total é:

M 0 T = M 0 y + M 0 x = 4   k N   s e n   60 ° ⋅ x   m - 4   k N cos ⁡ 60 ° ⋅ 1,5   m

Mas como tínhamos calculado antes, essa expressão acima tem que ser 80   k N ⋅ m

Assim:

4   k N   s e n   60 ° ⋅ x   m - 4   k N cos ⁡ 60 ° ⋅ 1,5   m = 80   k N ⋅ m

⇒ x ⋅ s e n   60 ° - 1,5 ⋅ cos ⁡ 60 ° = 20

⇒ x ⋅ 0,86 - 1,5 ⋅ 1 2 = 20

⇒ x ⋅ 0,86 - 0,75 = 20

⇒ x = 20,75 0,86 = 24,1

Resposta

Logo x = 24,1   m cria o momento máximo.

O momento máximo = 80   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O torquímetro ABC é usado para medir o momento ou torque aplicado a um parafuso quando ele está localizado em A e uma força é aplicada à alça em C. O mecânico lê o torque na escala em B. Se uma extens
A força de 70 N age na extremidade do tubo em B. Determine (a) o momento dessa força em relação ao ponto A e (b) a intensidade e a direção de uma força horizontal, aplicada em C, que produz o mesmo mo
O elemento BC conectado à chave inglesa é usado para aumentar o braço de alavanca da chave, conforme mostra a figura. Se um momento em sentido horário MA = 120 N . m é necessário para apertar o parafu
A cancela de travessia da linha férrea consiste em um braço de 100 kg com um centro de massa em Ga e o contrapeso de 250 kg com um centro de massa em GW. Determine a intensidade e o sentido direcional
A força de 70 N age na extremidade do tubo em B. Determine os ângulos u (0° ≤ u ≤ 180°) da força que produzirão os momentos máximo e mínimo em relação ao ponto A. Quais são as intensidades desses mome