Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 165
O cabo suporta um carregamneto uniformemente distribuido ao longo da horizontal como mostra a figura. O ponto mais baixo está a à direita de . Determine (a) a distância vertical , (b) o comprimento do cabo, (c) os componemtes da reação em .
Passo 1
Bom galera, vamos começar analisando o somatório das forças no eixo vertical na porção do cabo:
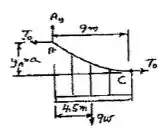
E o momento, adotando como o eixo de rotação:
Passo 2
Show de bola, agora na parte do cabo, a gente analisa o somatório das forças verticais:
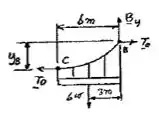
Então, a gente analisa o momento a partir de no cabo inteiro:
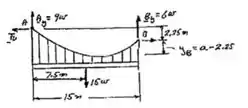
Passo 3
Belezinha, agora a gente pega aquela equação que a gente encontrou no passo 1 e substitui o valor de que acabamos de encontrar:
Resolvendo isso, encontramos:
Passo 4
Calma, tá quase acabando. Vamos calcular o comprimento do cabo:
Primeiro o comprimento do cabo :
E o comprimento em :
Então, o comprimento total do cabo é a soma:
Passo 5
Por fim, a gente pode encontrar as componente de com o que já temos:
E a componente horizontal: