Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 27
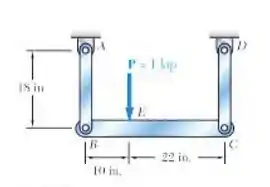
Cada uma das barras AB e CD é feita de alumínio e tem uma seção transversal com área de 0,2 Sabendo que elas suportam a barra rígida BC, determine o deslocamento do ponto E.
Passo 1
Fala aí galera tudo belezinha? Antes de mais nada partiu calcularmos o diagrama do corpo livre da seção BC.
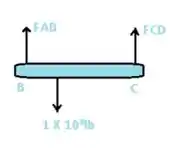
Calculando o somatório do momento em C temos...
E agora o somatório das forças em Y...
Gurizada falta pouco, após encontradas as forcas nas seções podemos determinar o alongamento na nossa velha e conhecida equação....
Passo 2
Agora para encontrarmos o deslocamento, vamos antes desenhar um diagrama esboço para antes determinamos a inclinação, venha cmg :D
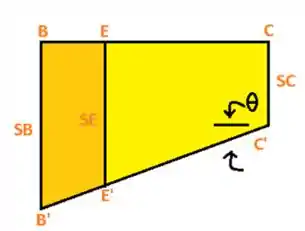
Inclinação:
Agora podemos determinar o deslocamento da seguinte maneira 😉
Resposta
Exercícios de Livros Relacionados
Um vaso esférico de pressão de 500 m m de diâmetro interno e 6,35 m m de espessura da parede é fabricado com um aço cuja a tensão última de tração é de 400M p a . Determinar o coeficiente de segurança
6.124 a 6.127 Para o estado plalno de deformação, usar o círculo de Mohr para determinar: (a ) a orientação e a intensidade das deformações específicas normais principais;(b) a máxima deformação espec
6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo θ , no sentido mostrado.
6.124 a 6.127 Para o estado plalno de deformação, usar o círculo de Mohr para determinar: (a ) a orientação e a intensidade das deformações específicas normais principais;(b) a máxima deformação espec
6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo θ , no sentido mostrado.