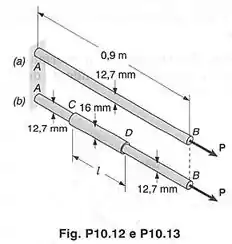
Cada uma das barras mostradas é feita de um aço com tensão de escoamento igual a e o módulo de elasticidade de . Sabendo-se que , determinar a máxima energia de deformação que pode ser absorvida em cada uma das barras, sem que cause qualquer deformação permanente.
Passo 1
Fala, galera bonita! Bora cair dentro de uma questão de energia de deformação?
A questão quer saber duas coisas: ela quer saber quanto vale a energia de deformação máxima que a barra pode absorver sem escoar e também quer saber qual é a energia de deformação máxima que a barra pode absorver sem escoar.
A figura abaixo mostra as informações mais importantes que temos para calcular e .
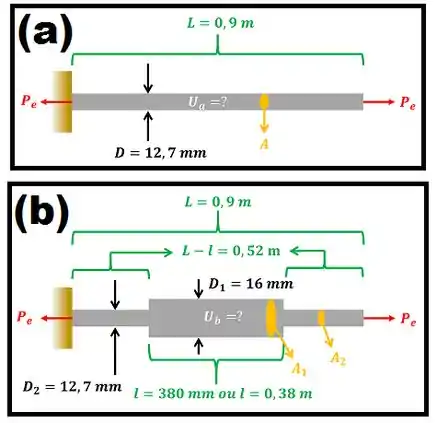
é a força que faz a barra começar a se deformar de forma permanente. Ou seja, é a força em que a barra começa a escoar. O da barra pode ser diferente do da barra .
Em outras palavras, é a força máxima que faz as barras e absorverem o máximo de energia! Para achar o da barra , temos que multiplicar pela área da barra .
onde é a tensão na qual a barra começa a se deformar permanentemente.
No entanto, para achar o da barra , temos que comparar a força que faz a parte grossa da barra escoar com a força que faz a parte fina da barra escoar.
A menor das duas será a força que faz a barra total escoar!
é a área da seção transversal da parte mais grossa da barra . é a área da seção transversal da parte mais fina da barra . Como é menor que , é menor que . Por isso:
Tá, mas como podemos calcular e a partir de ?
Como a barra tem área transversal constante, podemos usar a equação que calcula a energia de deformação de barras de área constante. Usaremos essa fórmula para calcular .
onde é o módulo de elasticidade do aço que vale segundo o enunciado.
Já a barra é formada por duas barras: a barra 2 de comprimento que tem área da seção transversal constante e igual a e a barra 1 de comprimento com área de seção transversal . Como a barra é formada por duas barras, sua energia de deformação é a soma entra as energias de deformação da barra 1 e da barra 2 .
Como essas duas barras têm áreas de seção transversal constantes, podemos usar a fórmula 10.14 do livro que calcula as energias de deformação e delas.
Substituindo e na equação de :
Agora que temos todas essas informações em mãos, vamos calcular a energia de deformação da barra no próximo passo!
Passo 2
Nesse passo nós vamos resolver a letra (a) da questão. Ou seja, calcular a energia de deformação da barra completa. Para isso, precisamos achar a área em .
Além disso, temos que calcular a força em newton que faz a barra começar a escoar.
Antes, precisamos lembrar que a tensão vale .
Por fim, temos que converter de para , multiplicando por .
Substituindo esses valores na equação de :
Passo 3
Nesse passo nós vamos resolver a letra (b) da questão, calculando .
Para calcular precisamos conhecer as área e em .
Além disso, precisamos achar da barra em newton .
Substituindo esses valores na outra fórmula de , achamos: