Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 93a
Uma força axial e cenrada, de intensidade , é aplicada à barra de aço mostrada. Determinar o máximo valor da tensão normal. (a) em A; (b) em B
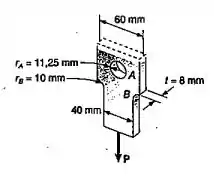
Passo 1
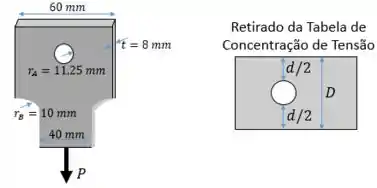
A questão pode ser resolvidade de forma direta. Observe o gráfico de Coeficientes de Concentração de Tensões no livro.
Para o caso de um furo precisamos calcular a propriedade .
E a razão
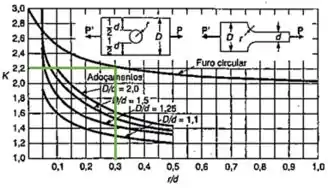
Observando o gráfico, o coeficiente de concentração de tensão será:
Passo 2
E agora é só calcular a tensão utilizando o coeficiente
Primeiro calculamos a área de seção transversal. Não esquece de considerar o furo!
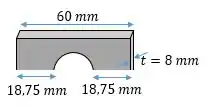
E calculamos a tensão:
A tensão é:
Resposta
Exercícios de Livros Relacionados
O eixo maciço de aço mostrado está submetido aos torques de 0,9k N × m , aplicados nas extremidades A e D . Usando G = 77G P a , determinar a energia de deformação do eixo.
Para o estado de tensões mostrado na Fig. a, determinar as tensões sobre um elemento orientado como mostrado na Fig. b. Calcular a densidade de energia de deformação específica, inicialmente dado pelo
Mostrar, por integração, que a energia de deformação da barra A B , em forma de tronco de cone, é U = 7 24 T 2 L G J m í n í onde J m í n í é o momento de inércia polar da seção transversal da barra,
Um cilindro vazado de borracha liga uma barra A , de raio R 1 , a um tubo B , de raio interno R 2 , formando um suporte isolante de vibração. Denotando por G o módulo de elasticidade transversal da bo
Determinar a energia de deformação da barra prismática A B , levando em conta os efeitos das tensões normais e das tensões cisalhantes.