Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 30

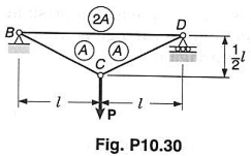
Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga é aplicada.

Passo 1

Oi, gente! Tudo bem com vocês? Bora fixar nosso conhecimento sobre energia de deformação?

Nessa questão, vemos as treliças , e suportando uma força . Essa força faz as treliças , e se deformarem. Por isso, a treliça absorve a energia de deformação e a treliça absorve a energia de deformação e a treliça absorve a energia . O enunciado quer saber quanto vale a energia de deformação total que é a soma das três.

Podemos ver na figura abaixo que, como a treliça é forçada com a carga , ela reage com uma força . O mesmo ocorre com as treliças e . Elas sofrem os efeitos da força e reagem com as forças e . É MUITO importante notar que as forças de reação das treliças , e estão SEMPRE na mesma direção das treliças!

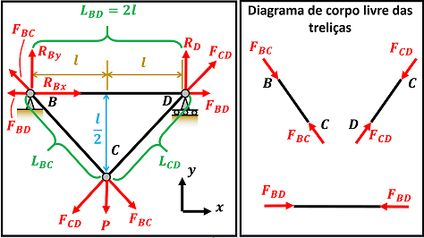
Note que o ponto tem duas forças de reação e e o ponto só tem uma reação . Isso ocorre, porque o ponto está impedido de se mover em e em , enquanto o ponto só está impedido de se mover na direção .

Para descobrir quanto vale , e precisamos aplicar duas equações de equilíbrio de forças nos ponto e . E por que não aplicamos essas equações no ponto ?

Porque o ponto tem duas reações e desconhecidas e o ponto só tem uma .

A equação do equilíbrio no eixo para os pontos e é:

onde são as componentes horizontais das forças.

Também vamos aplicar a equação de equilíbrio no eixo nesses dois pontos e !

onde são as componentes verticais das forças.

Achar as forças , e é fundamental para achar , e .

, e são calculadas usando a equação 10.14 do livro. Essa equação é válida para barras com áreas da seção transversal constantes, como é o nosso caso!

é o módulo de elasticidade das treliças. O módulo de elasticidade das duas treliças são iguais, porque o enunciado diz que elas são feitas do mesmo material. , e são as áreas das seções transversais das treliças. e são iguais a e é igual a como mostra a Fig. 10.30.

Mesmo com essas informações em mão, ainda precisamos calcular o seno e cosseno de um ângulo presente no problema para poder usar as equações de equilíbrio.

Passo 2

Nesse passo, nós vamos calcular o seno e o cosseno do ângulo presente no problema.

Veja a figura abaixo para entender que ângulo é esse.

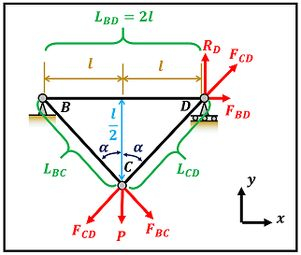
Antes de tudo, precisamos calcular os comprimentos e através do teorema de Pitágoras!

Para calcular o seno do ângulo , temos dividir o lado oposto ao ângulo pela hipotenusa .

Para calcular o cosseno do ângulo , temos dividir o lado adjacente ao ângulo pela hipotenusa .

Passo 3

Vamos começar o cálculo das forças fazendo o equilíbrio de forças na vertical e horizontal no ponto .

Começamos pelo ponto , porque ele tem apenas duas forças que não conhecemos: e . O ponto tem 3 forças desconhecidas: , e .

Para fazer o equilíbrio vertical, vamos ver quanto vale a projeção de e de em .

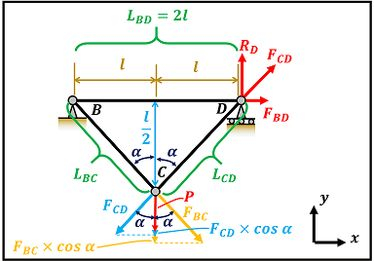
Através da figura acima vemos que existem três forças em : a projeção de , a projeção de e a força . Como a força , a projeção de e a projeção de estão pra baixo, colocaremos um sinal de menos na frente delas na equação de equilíbrio em .

Agora vamos fazer o equilíbrio de forças na horizontal no ponto .

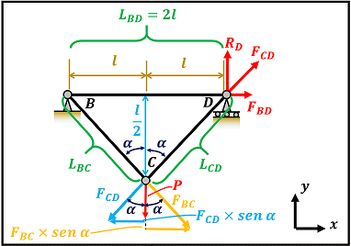
Através da figura acima vemos que existem apenas duas forças em : a projeção da força e a projeção da força . não tem projeção no eixo . Como a projeção da força está para a direita, colocaremos um sinal de mais na frente dela. Como a projeção da força está pra esquerda, colocaremos um sinal de menos na frente delas na equação de equilíbrio em .

Substituindo o valor de na equação de que encontramos antes, achamos:

Substituindo , na equação que achamos com o equilíbrio de forças em :

Só falta calcular para a gente passar para a etapa de calcular as energias!

Passo 4

Nesse passo, vamos calcular a força através das equações de equilíbrio em e no ponto .

Para fazer o equilíbrio vertical, vamos ver quanto vale a projeção de em .

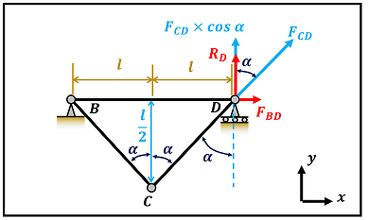
Através da figura acima vemos que existem duas forças em : a projeção de e a reação . Como e a projeção de estão pra cima colocaremos um sinal de mais na frente delas na equação de equilíbrio em .

Substituindo nessa equação:

Agora vamos fazer o equilíbrio de forças na horizontal no ponto .

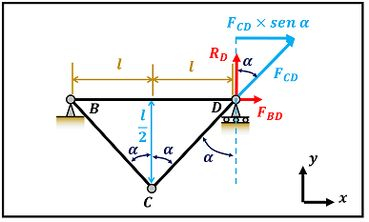
Através da figura acima vemos que existem apenas duas forças em : a projeção da força e . não tem projeção no eixo . Como a projeção da força e a força estão para a direita, colocaremos um sinal de mais na frente delas.

Substituindo o valor de na equação acima, achamos:

Agora temos as três forças que precisamos para calcular , , e .

No próximo passo faremos essa conta.

Passo 5

Nesse passo calcularemos , , e .

Vamos começar calculando .

Lembrando que o comprimento da treliça vale , que a área da seção transversal dessa treliça vale e que vale achamos:

Já achamos uma energia. Agora vamos partir para o cálculo de . Para isso, devemos lembrar que o comprimento da treliça vale , que a área da seção transversal dessa treliça vale e que vale .

Por fim, temos que calcular a valor da energia . Para isso, devemos lembrar que o comprimento da treliça vale , que a área da seção transversal dessa treliça vale e que vale .