Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 111

Cada uma das duas barras de latão mostradas está sujeita a um torque de intensidade T = 1,4   k N m . Sabendo-se que G = 39 G P a , determinar para cada barra a máxima tensão de cisalhamento e o ângulo de torção em B.

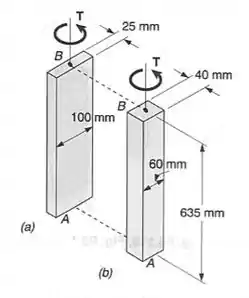
Passo 1

Para resolvermos esse tipo de problema, temos que lembrar que para barras retangulares a fórmula de cálculo é diferente, e com isso temos que lembrar que a nossa fórmula funciona da seguinte maneira:

τ m a x = T C 1 a b 2

Ф = T L C 2 a b 3 G

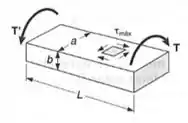
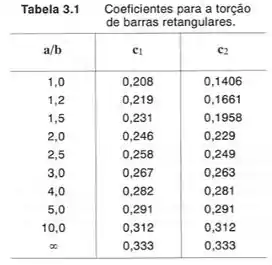
Pelo enunciado temos que:

T = 1400   N m

G = 39 G P a

Passo 2

Agora para o primeiro item eles pedem a tensão cisalhante máximo, podemos usar a nossa fórmula.

τ m a x = T C 1 a b 2

Agora vamos verificar cada uma das barras:

  • Barra tipo A

    • a b = 100 25 = 4

    C 1 = 0,282

    a = 100   m m

    b = 25   m m

    T = 1400   N m = 1400000   N m m

    Substituindo teremos que:

    τ m a x = T C 1 a b 2 = 1400000   [ N m m ] 0,282   .     100   .   25 2   [ m m 3 ] = 79,43   M P a

  • Barra tipo B

    • a b = 60 40 = 1,5

    C 1 = 0,231

    a = 60   m m

    b = 40   m m

    T = 14 00   N m = 14 00000   N m m

    Substituindo teremos que:

    τ m a x = T C 1 a b 2 = 1400000   [ N m m ] 0,231   .     60   .   40 2   [ m m 3 ] = 63,13   M P a

    Passo 3

    Agora para o segundo item eles pedem o ângulo de torção, podemos usar a nossa fórmula.

    Ф = T L C 2 a b 3 G

    Agora vamos verificar cada uma das barras:

  • Barra tipo A

    • a b = 100 25 = 4

    C 2 = 0,281

    a = 100 m m

    b = 25   m m

    L = 635   m m

    T = 1400   N m = 1400000   N m m

    G = 39   G P a = 39000   M P a = 39000   N m m 2

    Substituindo teremos que:

    Ф = T L C 2 a b 3 G = 1400000   N m m   .     635   [ m m ] 0,281   .     100   .   25 3   m m 4   .   39000   N m m 2   = 0,0519   R a d

    Passando para graus teremos que:

    Ф = 0,0 519   .   180 π = 2,97 °

  • Barra tipo B

    • a b = 60 40 = 1,5

    C 2 = 0,1958

    a = 60   m m

    b = 40   m m

    L = 635   m m

    T = 1400   N m = 1400000   N m m

    G = 39   G P a = 39000   M P a = 39000   N m m 2

    Substituindo teremos que:

    Ф = T L C 2 a b 3 G = 1400000   N m m   .     635   [ m m ] 0,1958   .     60   .   40 3   m m 4   .   39000   N m m 2   = 0,0303   R a d

    Passando para graus teremos que:

    Ф = 0 , 0303   .   180 π = 1,74 °

    Resposta

  • Barra A

    • τ m a x = 79,43   M P a

    Ф = 2,97 °

  • Barra B

τ m a x = 63,13   M P a

Ф = 1,74 °

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo sólido mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar o ângulo de torção causado pela aplicação de um torque T1 = 9 kN.m e T2 = 14,7 kN.m.
Uma barra de aço é usinada no feitio mostrado, constituindo um eixo com a forma de um tronco de cone, no qual troques de intensidade T = 8,5 kN.m são aplicados. Considerando que o aço é elastoplástico
Uma barra de aço é usinada no feitio mostrado, constituindo um eixo com a forma de um tronco de cone, no qual troques de intensidade T = 8,5 kN.m são aplicados. Considerando que o aço é elastoplástico
O eixo sólido mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar a intensidade do torque T, para que a zona plástica tenha 6,35 mm e 19 mm de profundidade.
Um eixo vazado mostrado é feito de um aço doce, o qual se considera ser elastoplástico com G = 77 GPa e τ=145MPa. Determinar a intensidade do torque T.