Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 123
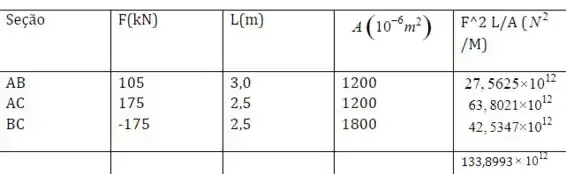
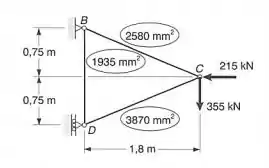
Cada um dos membros da treliça mostrada é feita de aço e tem a área da seção transversal indicada. Usando-se , determinar a deflexão horizontal do nó C.
Passo 1
Legal!! Vamos dar um bizu no nó C!
Lá a gente tem que:
Abrindo nossas forças no eixo :
Maneiro! Vamos olhar para o eixo agora!
Colocando nossas forças, a gente tem:
Passo 2
Com as nossas duas equações aqui de cima, a gente tem um sistema com duas incógnitas! Vamos resolver ele!
Olhando para primeira equação, temos:
Dividindo os dois lados por ,
Substituindo na segunda equação, temos:
Logo,
Vamos olhar para o nó B agora!
Como a gente já descobriu os valores das forças e , fica:
Passo 3
Resposta
Exercícios de Livros Relacionados
Determine a variação da altura e a variação do volume para a barra de comprimento 150mm, considerada no Porb 2.66.
Duas barras de aço maciças, cada uma com 56mm de diâmetro, são soldadas juntas para formar o suporte mostrado. Usando E = 200 GPa e G = 77 GPa, determinar a deflexão vertical do ponto C.
Resolver o prob. 10,140 assumindo que a porção AB da prancha de trampolim tem 2,85 m e que a porção BC tem 0,75 m de comprimento
Três membros de mesmo material e mesma área da seção transversal são usados para suportar a carga P. Determinar a força em cada membro, quando 0 = 30 °