Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 136
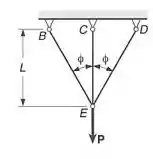
Três membros de mesmo material e mesma área da seção transversal são usados para suportar a carga P. Determinar a força em cada membro, quando
Passo 1
Começaremos destacando o membro BC no suporte C.
Adicione reação como carga
Passo 2
Junta C. F
Passo 3
+ +0
Resposta
Exercícios de Livros Relacionados
Duas barras de aço maciças, cada uma com 56mm de diâmetro, são soldadas juntas para formar o suporte mostrado. Usando E = 200 GPa e G = 77 GPa, determinar a deflexão vertical do ponto A.
A viga AB é simplesmente apoiada sofre um impacto em D devido a um bloco de massa m, que se desloca horizontalmente com uma velocidade v 0 . Mostrar que a tensão normal máxima resultante σ m na viga,
A montagem ABC é feita de um aço para o qual E = 200 G P A e σ e = 320 G P a . Sabendo-se que uma energia de deformação de 5J deve ser absorvida pela montagem, assim que a carga axial P é aplicado, de
Duas placas de cobertura são soldadas a uma viga de perfil laminado de aço, como mostrado. Usando-se E = 29 MPa, determinar a declividade e a deflexão do ponto C.
Resolver o prob; 10,146 assumindo que o comprimento BC das placas é de cobertura reduzido para 1,2 m.