Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas de Revisão - Ex. 144

Duas barras de aço maciças, cada uma com 56mm de diâmetro, são soldadas juntas para formar o suporte mostrado. Usando E = 200 GPa e G = 77 GPa, determinar a deflexão vertical do ponto C.

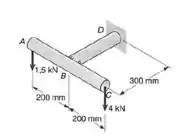
Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

considere a torção da haste CD (180 N=P)

φ c = T L G J = P a b G J

y A I = - a φ c = P a 2 b G J

considere a curvatura da haste CD

y A I I = y B I I = y c I I = P b 3 3 E I

Passo 2

considere a curvatura da haste AC

y A I I I = - P a 3 3 E I

por superposição

y A = y A I + y A I I

= P a 2 b G J - b 3 3 E I

Passo 3

Dados:

G = 77 × 10 9   P a ,     J = π 2   c 4 = π 2 12 4 = 32,572 × 10 3 m m 4 = 32,572 × 10 - 9 m 4

E = 200 0 × 10 9   P a ,     I = 1 2 J = 16,286 × 10 - 9 m 4

G J = 846,87   N . m 2     E I = 1140,02   N . m 2

a = 0,5 m ,       b = 0,4 m

y A = 180 - 0,5 2 0,4 846,87 - 0,4 3 3 1140,02 - 0,5 3 3 1140,02 = - 31,2 × 10 - 3 m

= 31,2 m m ↓

y B = 180 - 0,5 2 0,4 846,87 - 0,4 3 3 1140,02 = 17,89 × 10 - 3 m

= 17,89 m m ↑

Resposta

17,89 m m

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a barra uniforme com o carregamento mostrado e usando o teorema de Castigliano, determinar a deflexão no ponto B
Três barras, todas com a mesma rigidez flexional EI, são soldadas para formar a estrutura ABCD. Para a carregamento mostrado, determinar : (a) a deflexão do ponto D; (b) o declive, em relação à vertic
Determinar a reação no apoio móvel para a viga com o carregamento indicado.
Para a barra uniforme com o carregamento mostrado e usando o teorema de Castigliano, determinar: (a) a deflexão horizontal no ponto B; (b) a deflexão vertical no ponto B.
Para a viga uniforme com o carregamento mostrado, determinar a reação em cada um dos apoios.