Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 135
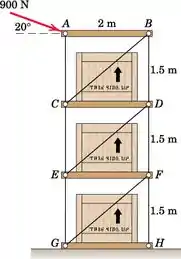
Cada uma das plataformas horizontais de um rack de armazém tem uma massa de 20 kg e carrega uma caixa de 180 kg localizada no centro. As plataformas são suportadas por membros de duas forças de massa desprezível, conforme mostrado. Se o rack estiver sujeito a uma força de 900-N em A, determine as forças nos membros CE, DE e DF.
Passo 1
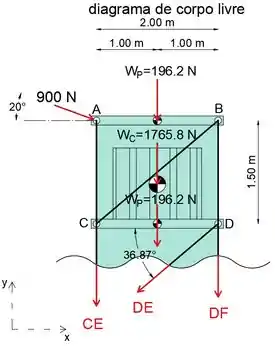
Vamos cortar os membros CE, CD e DF e analisar a parte superior da treliça. Observe que como não há nenhum suporte (força desconhecida) colocado na parte superior, teremos apenas três forças desconhecidas (CD, CE e DF) atuando no sistema, que podem ser determinadas a partir de equações de equilíbrio.
O ângulo que o membro DE faz com a horizontal é:
O peso da caixa é:
O peso da placa é:
Passo 2
Observe que vamos supor que todos os membros desconhecidos estão em
compressão
Passo 3
Equacionando a soma dos momentos sobre o ponto D a zero, eliminaremos as forças de reação DE e DF, de modo que a única incógnita na equação será a força CE
A partir daqui, podemos expressar a força CE como:
Como obtivemos o resultado negativo, isso significa que o membro está em compressão
Ao igualar a soma das forças na direção x a zero, podemos determinar a força DE
A partir daqui, podemos expressar a força DE como:
Passo 4
Finalmente, ao igualar a soma das forças na direção y a zero, podemos determinar a força DF
A partir daqui, podemos expressar DF como:
Substitua CE e DE por seus valores
Como obtivemos o resultado negativo, isso significa que o membro está em compressão