Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 138
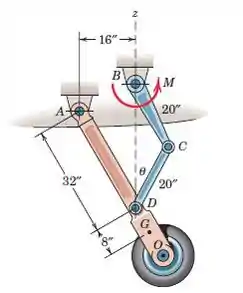
O conjunto da roda do nariz é elevado pela aplicação de um torque M para ligar BC através do eixo em B. Se o braço e a roda AO têm um peso combinado de 100 lb com centro de gravidade em G, encontre o valor de M necessário para levantar a roda quando D está diretamente abaixo de B, em cujo ângulo de posição θ é 30 ∘.
Passo 1
Primeiro, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre do braço parcial AO que faz com o ângulo do eixo z de
Observe que a roda está no ar, por isso não tem contato com o solo, ou seja, não tem uma força de reação
Ao igualar a soma dos momentos sobre o ponto A a zero, eliminaremos as forças de reação em A, para que possamos determinar a força CD
Passo 2
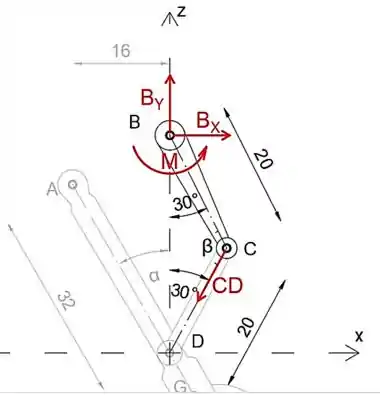
A seguir, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre do membro BC. Podemos notar que o triângulo △ BCD é isósceles, o que significa que o membro BC também faz o ângulo de 30∘ com o eixo z, ou seja, os membros BC e CD fazem o ângulo de
Passo 3
Ao igualar a soma dos momentos sobre o ponto B a zero, eliminaremos as forças de reação em B, para que possamos determinar o par M