Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 140
Todos os membros de duas forças da treliça carregada têm o mesmo comprimento. O membro BCD é uma viga rígida. Determine as forças nos membros BG e CG em termos da carga L.
Passo 1
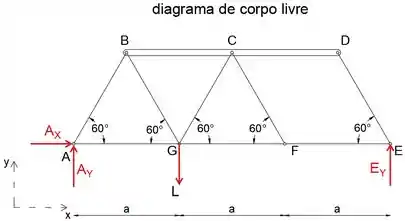
Primeiro, vamos desenhar o diagrama de corpo livre de toda a treliça para determinar as forças de reação em A e E
Observe que, uma vez que todos os membros de duas forças têm comprimento igual, eles formam triângulos equiláteros, o que significa que todos os membros diagonais formam com o ângulo horizontal de 60
Passo 2
Ao igualar a soma dos momentos sobre o ponto A a zero, podemos determinar a força de reação Ey,
Passo 3
Ao igualar a soma das forças na direção x e y a zero, podemos determinar as forças de reação em A
Substitua Ey pelo seu valor
Passo 4
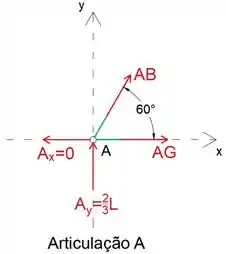
Em seguida, analisando a junta A, podemos determinar a força no membro AG
Observe que vamos supor que todos os membros desconhecidos estão em tensão
Passo 5
Substitua AB por seu valor
Passo 6
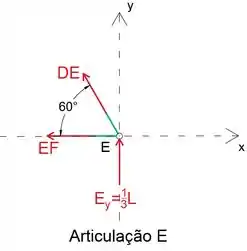
Em seguida, analisando a junta E, podemos determinar a força no membro EF
Observe que vamos supor que todos os membros desconhecidos estão em tensão
Passo 7
Substitua DE por seu valor
Finalmente, vamos analisar a junta G a fim de determinar as forças nos membros BG e CG
Ao igualar a soma das forças na direção x a zero, escreveremos a força BG como função de CG
A partir daqui, podemos expressar BG como:
Passo 8
Equacionando a soma das forças na direção y a zero, obteremos a equação em que CG é a única incógnita
Substitua BG pela expressão (1)
A partir daqui, podemos expressar CG como:
Finalmente, substitua CG por seu valor na expressão (1) para calcular a força no membro BG