Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 25
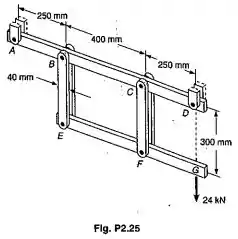
Cada uma das quatro hastes de ligação verticais, conectadas às duas vigas horizontais, são de alumínios e têm uma seção transversal retangular de . Para o carregamento mostrado, determinar a deflexão no (a) ponto E; (b) ponto F; (c) ponto G.
Passo 1
Vamos fazer um desenho esquemático da estrutura:
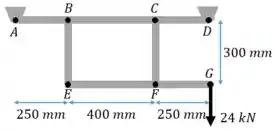
Não precisamos calcular todas as reações. Como só estamos interessados nos pontos E, F e G, podemos fazer uma seção considerando apenas a barra .
Como os pontos e são pinos não existe momento nestes pontos, apenas forças.
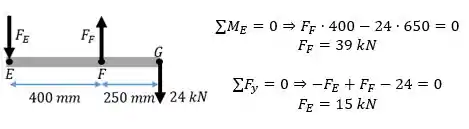
Passo 2
Aqui temos a pegadinha da questão. Tanto no ponto quanto no ponto temos duas barras! Então a área de seção transversal será dobrada.
Passo 3
Agora temos todos as forças que nos interessam. Utilizando a Equação 2.7 do livro, vamos calcular a deformação nas barras AB e BE.
Para a gente não se confundir, não vamos usar o sinal negativo. Mas tenha em mente que a força em E é uma compressão:
E que a força em F é tração:
Passo 4
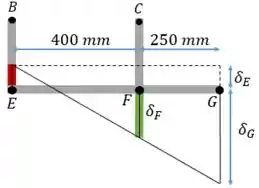
Utilizando as deformações do ponto E e D podemos calcular o deslocamento do ponto G. Na figura abaixo a gente representou a compressão de E em vermelho e o alongamento de F em verde.
Então dá para usar semelhança de triângulo para calcular o deslocamento no ponto G
