Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 37
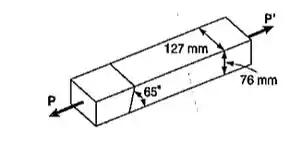
Sendo a máxima tensão de tração admissível para a emenda colada do Prob. 1.36 igual a 415KPa, determine: (a) a maior carga axial P que pode ser aplicada; (b) a correspondente tensão de cisalhamento nessa emenda.
Passo 1
Precisamos primeiro saber a área que a tensão vai atuar. Vamos desenhar e observar.
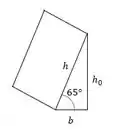
A força vai atuar no plano oblíquo e precisamos da altura h, que é calculada dessa forma.
Passo 2
A força normal precisa ser perpendicular ao plano, então a gente vai decompor ela:
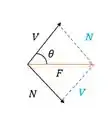
E a tensão normal de tração é:
Resolvendo, temos P:
Passo 3
Para a tensão cisalhante a ideia é parecida, precisamos decompor a força na outra direção.
A área de atuação é a mesma, então:
Resposta
Exercícios de Livros Relacionados
A barra de ligação horizontal BC é de 6,35 m m de espessura, tem uma largura w = 31,8m m e é feita de aço com tensão última de tração igual a 483M P a . Qual deve ser o coeficiente de segurança a ser
As barras AB e BE da treliça mostrada são da mesma liga metálica. Sabe-se que uma barra de 20 m m de diâmetro desta mesma liga foi testada até a falha e foi registrada uma carga máxima de 150k N . Usa
As barras AB e BE da treliça mostrada, são da mesma liga metálica. Sendo que a barra AB tem um diâmetro de 28 m m e que a carga máxima para a barra é de 300k N , determine:O coeficiente de segurança p
Para a emenda e carregamento do P r o b .1.36 , determine o coeficiente de segurança, sabendo-se que a resistência ultima da cola é de 1035k P a na tração e 1475k P a no cisalhamento.
Quatro parafusos de aço são usados para prender a placa mostrada à viga de madeira. Admitindo que a tensão de cisalhamento última para o aço utilizado é de 345M p a , e desejando um coeficiente de seg