Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 33
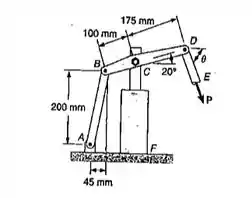
O cilindro hidráulico CF, que controla parcialmente a posição da barra cilíndrica DE, está completamente distendido na posição mostrada. A barra BD tem 15mm de espessura e está ligada em C, por um parafuso de 9mm de diâmetro. Sabendo-se que P=2KN e , determine: (a) a tensão de cisalhamento média no parafuso; (b) a tensão de esmagamento em C, na barra BD.
Passo 1
O item (a) pede a tensão cisalhante no pino C. Vamos começar fazendo um diagrama de corpo livre da nossa barra BD, pois tudo dependerá disso.
Nossa meta aqui vai ser a seguinte: decompor os esforços na horizontal e vertical e usar as equações de equilíbrio, ok?
Eu nomeei pra gente as reações nos pinos de B e D, e no parafuso de C. Vamos olhar essa reação B.
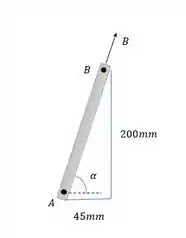
Vamos decompor a força seguinte esse ângulo . Primeiro vamos calcular o tamanho da barra AB.
Vamos chamar de a força horizontal e de a força vertical.
Passo 2
Bora olhar para a outra força, agora no pino D. Vamos decompor ela da mesma maneira.
Agora a gente pode fazer o somatório dos momentos no ponto C, e encontraremos as reações em B, que nos ajudarão a encontrar a reação em C. Aqui precisaremos decompor também as distâncias. Aqui consideraremos o sentido anti-horário positivo.
Substituindo os valores e resolvendo a equação a gente vai ter o seguinte:
Passo 3
Agora que encontramos as reações em B, podemos fazer o somatório das forças na barra e encontraremos as reações em C.
Agora o somatório das forças verticais.
A reação resultante em C é:
Passo 4
Finalmente para o item a, agora é só calcular a área do parafuso e descobriremos logo a tensão cisalhante. Lembrando que o parafuso tem uma só área resistindo ao cisalhamento, assim:
E enfim:
Passo 5
O item b, pede a tensão de esmagamento que vai ocorrer na barra no ponto C.
A área onde o esmagamento ocorre é justamente por onde o pino passa na barra. Assim: