Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 26
Duas pranchas de madeira, cada uma com 15mm de espessura e 200mm de largura, são unidas por uma respiga de união colada, como indicado. Sabendo-se que esta junta irá falhar, quando a tensão de cisalhamento média na cola atingir 900KPa, determine o comprimento necessário d, se a junta deve resistir a uma carga axial de intensidade P= 4KN.
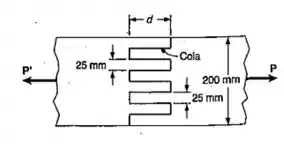
Passo 1
Bora ver o desenho que a gente tem e avaliar quais são os pontos possíveis que possam ocorrer cisalhamento. Lembrando que o cisalhamento acontece nas áreas que são paralelas a força.
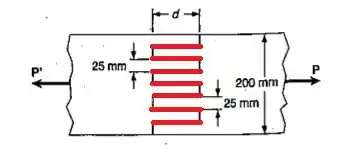
Observando bem, dá pra ver que temos 7 áreas paralelas à força que são importantes. Se liga que elas devem pertencer à mesma seção analisada, nós não poderíamos pegar essas 7 áreas da frente e juntar com as de trás.
Sei que olhando de frente as áreas parecem apenas linhas mas elas estão dentro da peça e podem ser calculadas assim:
Onde , a espessura da peça e é a dimensão que queremos saber.
Presta muita atenção agora, a força vai se dividir por todas as áreas que forem paralelas.
Assim temos que levar em consideração as 7 áreas, então.
Passo 2
Já colocamos a área em função da dimensão que a gente quer e agora é só usarmos a equação da tensão cisalhante.
Vamos substituir os valores mas antes passaremos para unidades mais interessantes. A carga está em , vamos multiplicar por e passar para . Faremos o mesmo com a tensão, ela está em , vamos multiplicar por e passar para .
E enfim: