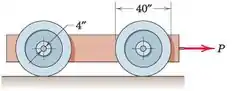
Cada uma das quatro rodas do veículo pesa 40 libras e é montada em um mancal de 4 pol. De diâmetro (eixo). O peso total do veículo é de 960 libras, incluindo rodas, e é distribuído igualmente nas quatro rodas. Se uma força P = 16 lb for necessária para manter o veículo rodando a uma velocidade baixa constante em uma superfície horizontal, calcule o coeficiente de atrito que existe nos rolamentos das rodas. (Dica: desenhe um diagrama de corpo livre completo de uma roda.)

Equacionando a soma das forças na direção x e y a zero, podemos determinar as forças de reação N e F

Próximo. vamos isolar e desenhar o diagrama de corpo livre da roda, com seu peso, forças de reação do solo e força de reação do eixo atuando nela

Equacionando a soma das forças nos eixos x e y a zero, podemos determinar os componentes do R resultante

Usando o teorema de Pitágoras, podemos calcular a magnitude da resultante

Equacionando a soma dos momentos sobre o centro do eixo (vamos chamá-lo de ponto O) a zero, podemos determinar a distância entre o R resultante e o ponto O (raio de fricção rf)

Sabemos que o raio do círculo de atrito rf é igual ao produto do raio do eixo e do seno do ângulo de atrito

A partir daqui, podemos escrever a expressão para o ângulo de fricção

Vamos colocar os valores de r e rf na equação

Finalmente, podemos determinar o coeficiente de atrito usando a expressão: