Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 102
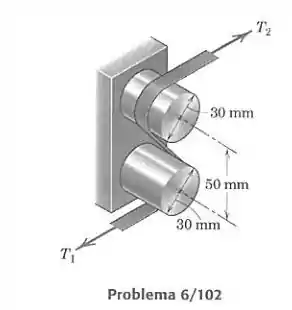
A fita desliza em volta dos dois eixos fixos, como mostrado, e está sob a ação de forças trativas horizontais N e N. Determine o coeficiente de atrito entre a fita e os eixos.
Passo 1
Considerando que a fita esteja em equilíbrio, ou seja, se desloca sob velocidade constante, podemos aplicar a fórmula do equilíbrio para cordas enroladas em torno de uma superfície:
Sendo e as trações maior e menor nas extremidades da fita, o coeficiente de atrito entre a fita e as superfícies cilíndricas e o ângulo total de contato da fita com a superfície. Aplicando a fórmula, seremos capazes de encontrar .
Passo 2
Já temos os valores de N e N, então só falta o valor de para encontrar . Vamos olhar para a fita perpendicularmente aos eixos dos cilindros, para ter melhor noção do desenho e descobrir qual é o ângulo total:
Como a distância entre os centros é 50 mm e o raio é 15 mm, o segmento entre os círculos tem mm, e a metade dele tem então 10 mm. Nosso ângulo é igual a duas vezes o ângulo mostrado na figura. O ângulo por sua vez é determinado através de :
Descobrimos através de seu cosseno. Usamos os valores dos ângulos em radianos
Então achamos e :
Passo 3
Agora podemos aplicar a fórmula: