Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 198

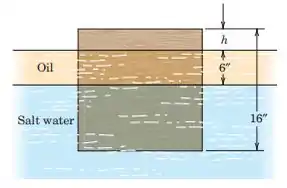
Um bloco de madeira na forma de um impermeabilizado de 16 pol. cubo está flutuando em um tanque de água salgada com uma de 6 pol. camada de óleo flutuando na água. Suponha que o cubo flutua na atitude mostrada e calcule o altura h do bloco acima da superfície do óleo. Os pesos específicos de óleo, água salgada e madeira são 56, 64 e 50   l b /   f ² , respectivamente.

Passo 1

E ai gurizada tudo belezinha???

Primeiro, vamos desenhar o diagrama de corpo livre do bloco.

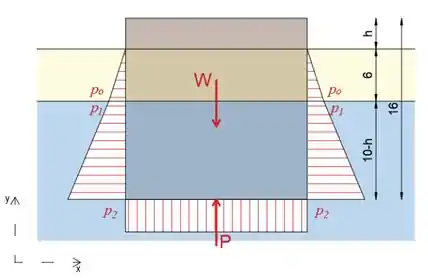
Observe que o peso do bloco é:

W = V b l o c k ∙ γ w o o d

Cada lado do bloco é 16 12 = 1.333 - f t longo, enquanto o peso específico da madeira é dado.

W = 1.333 ∙ 50 = 118.52   l b

Observe também que substituímos a pressão p 2 agindo na parte inferior do bloco por sua resultante.

P = p 2 ∙ A Onde A é a área de um lado do bloco.

P = p 2 ∙ 1.333 ²

P = 1.778   p 2

Passo 2

Ao igualar a soma da força na direção y a zero, podemos determinar a força P, i.e. pressão p 2 .

∑ F y = 0

W - P = 0

P = W

Substitua P e W pelo redator de valores na etapa acima.

1.778   p 2 = 118.52

⇒ p 2 = 118.52 1.778 = 66.67   l b / f t ²

Passo 3

Considere o esboço da etapa 1 mais uma vez. Para que o sistema esteja em equilíbrio, a pressão no óleo no fundo p 0 deve ser igual à pressão na superfície da água p 1 .

p 1 = p 0

Uma vez que a camada de óleo é 6 ´ ´ = 0.5   f t espessa, a pressão p 0 na parte inferior pode ser expressa como:

p 0 = 0.5 γ   o i l

p 0 = 0.5 ∙ 56 = 28   l b / f t ³

Portanto, a pressão da agua p 1   é: p 1 = p 0 = 28   l b / f t ³

Passo 4

Agora considere a pressão atuando na parte inferior do bloco. Uma vez que a pressão na superfície da água é conhecida, podemos expressar a pressão em

10 - h i n .   = ( 10 - h ) / 12   f t           a profundidade é:

p 2 = p 1 + ( 10 - h ) 12   y  

Substitua p 1 , p 2 e por seus valores

66.67 = 28 + ( 10 - h )

Resposta

h = 2.75 ' '

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Depois de nivelar um lote, um construtor coloca quatro estacas para indicar os cantos da base para uma casa. Para prover uma base nivelada firme, o construtor coloca um mínimo de 75 mm de brita abaixo
Determine o centróide do sólido obtido pela rotação da área sombreada da figura em torno da linha x = h .
Determine por integração direta os valores de x - para os dois sólidos obtidos passando-se um plano de corte vertical através da forma dada na Fig. 5.21. O plano de corte é paralelo à base da forma da
Sabendo que dois topos iguais foram removidos da esfera de madeira de diâmetro 250 mm, determine a área total da superfície da parte restante.
Determine por integração direta o centroide da área mostada na figura. Demonstre sua resposta em termos de a e h .