Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 115
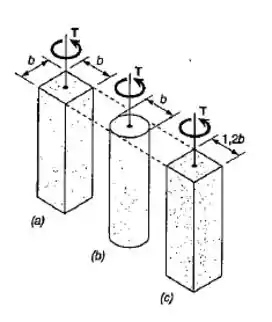
Cada uma das três barras de aço mostradas na figura deve ser girada por um ângulo de . Sabendo que b=30 mm, e G=27 GPa, determine o menor comprimento admissível para cada barra.
Passo 1
Bom, pra ficar mais organizadinho, vamos escrever de início o que nós temos:
Para a barra quadrada e para a retangular temos a relação
Se nós dividirmos e segunda equação pela primeira (com o objetivo de elimiar o T) teremos
Isolando o L, já que é o que a questão quer da gente
Passo 2
a) Para determinar o menor comprimento da primeira barra (base quadrada) precisamos inicialmente encontrar a realção entra a e b para encontrarmos os valor de na tabela 3.1:
Então, pela tabela 3.1 temos
Temos então pela fórmula que deduzimos no passo anterior
Agora fazemos o mesmo as outras barras.
Passo 3
b) agora trabalhando com a barra de base circular:
Como estamos lidando com um círculo temos pela teoria que a relação entra c e b é dada por:
Vamos descobrir o valor desse L ai pelas relações abaixo
Se, assim como no passo 1, dividirmos para eliminarmos T, e em seguida isolarmos L, temos
Passo 4
c) Vamos ver entaõ qual a dimensão necessária de L pra última barra (base retangular):
Então, pela tabela 3.1 temos
Trazendo a relação que encontramos no passo 1 para L
perfeitinho!