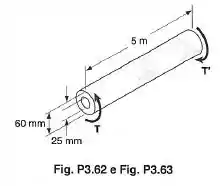
O eixo vazado de aço mostrado (, ) gira a Determinar: (a) a máxima potência que pode ser transmitida; (b) o correspondente ângulo de torção do eixo.

Vamos começar arrumando a unidade dos nossos dados. Para transformar a velocidade em para a frequência em , usamos a relação:

Logo,

A gente consegue escrever uma relação entre a tensão admissível e o torque produzido nessa situação, pela expressão:

E conseguimos escrever a potência produzida por um torque e uma frequência pela expressão:

Substituindo uma expressão na outra:

Para um eixo vazado, temos que:

Substituindo isso na nossa expressão para a potência:

Agora a gente consegue substituir os dados do nosso problema:

b) Agora a gente quer achar o ângulo de torção produzido nessa situação. Para isso usamos:

Vamos lembrar que:

Substituindo isso na expressão do ângulo de torção:

Substituindo os dados do problema:

Lembrando que para passar de radianos para graus é só multiplicar por .