Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 21
As caixas e pesam e , respectivamente. Elas estão conectados por um cabo e colocadas no plano inclinado. Se o ângulo for aumentado gradualmente, determine quando as caixas começarem a deslizar. Os coeficientes de atrito estático entre as caixas e o plano são e .
Passo 1
O problema pede que encontremos o ângulo máximo antes do movimento.
Beleza, vamos começar fazendo um diagrama de corpo livre em , e vamos decompor a força Peso, assim:
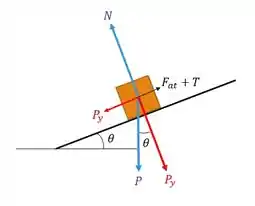
Primeiro a gente pega as forças perpendiculares ao plano inclinado:
Bom, você já deve saber, mas o atrito age em relação a normal, então a gente multiplica a normal com o coeficiente de atrito:
E a gente está estudando um corpo em equilíbrio, né?
Pois, a gente percebe que tem que ser igual ao atrito somado com a tração da corda, aí você pensa que complica mas calma aí e vamos para matemática que vai ficar mais fácil:
Ainda não parece muito mais fácil eu sei, mas espera mais um pouco, a gente já tem uma equação com duas variáveis, vamos pro outro bloco pra ver o que a gente encontra.
Passo 2
Então, agora partiu bloco :
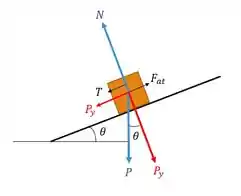
A gente faz do mesmo jeito:
Então a gente já calcula logo o atrito em :
Vamos ver se a resultante do peso paralela a inclinação agora pra ver se a gente acha outra equação pra usar:
E encontramos mesmo.
Passo 3
Então vamos montar um sistema com as equações:
Então somando as duas, a gente encontra:
Usando a função inversa trigonométrica na calculadora pra encontrar o ângulo :