Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 23
O depósito de papel toalha contém dois rolos de papel. O que está em uso é chamado de rolo principal e o outro é o rolo de apoio . Eles pesam e , respectivamente. Se os coeficientes de atrito estático nos pontos de contato e são e , determine a força vetorial inicial que deve ser aplicada ao papel no rolo principal a fim de puxar uma folha. O rolo principal é pinado no centro, enqunto o outro rolo não. Despreze o atrito no pino.
Passo 1
O problema pede que encontremos a força minima para que o deslocamento do papel comece.
Beleza, vamos começar fazendo o diagrama de corpo livre no rolo principal:
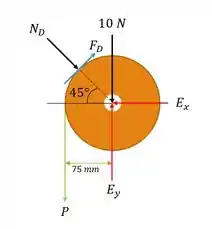
Bom, então olhando bem a força causa um momento então vamos analisar o momento nesse rolo:
Então, a gente precisa descobrir , que é causado pelo rolo .
E a gente sabe que o rolo é preso por um pino então não faz muito sentido a gente calcular as forças nele, vamos continuar então para o rolo .
Passo 2
Agora, a gente faz um diagrama de corpo livre no rolo .
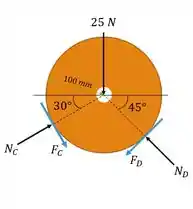
Analisando o momento nesse rolo fica:
Lembra do passo 1? Então agora a gente sabe que:
Então vamos analisar as forças, primeiro no eixo :
Então vamos substituir o pra ajudar:
Vamos usar agora o eixo para ver se a gente consegue algo:
Ou seja:
Passo 3
Agora sim, vamos usar o atrito:
Então substituindo nas equações que já temos e montamos o sistema:
Resolvendo as equações a gente encontra: