Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 77
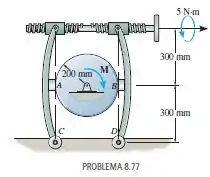
O mecanismo de freio consiste em dois braços com pinos e um parafuso de rosca quadrada com
roscas esquerda e direita. Assim, quando girado, o parafuso aproxima os dois braços. Se o avanço do parafuso é , o diâmetro médio é e o coeficiente de atrito estático é , determine a tração no parafuso quando um torque de é aplicado para apertá-lo. Se o coeficiente de atrito estático entre as pastilhas de freio A e B e o eixo circular é , determine o torque M máximo que o freio pode resistir.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Sabemos que o ângulo de fricção é dado por:
Portanto:
O ângulo de avanço do parafuso é dado por:
Substituindo os dados, temos que:
Passo 2
Agora vamos calcular o menor torque necessário para afrouxar o parafuso. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
58- O coeficiente de atrito estático μ s entre o corpo de 100k g e a cunha com ângulo de 15 ° vale 0.20 . Determine o módulo da força P necessária para levantar o corpo de 100k g se a ) rolamentos com
61- As duas cunhas com ângulo de 4 ° são usadas para posicionar a coluna vertical sob uma carga L . Qual é o menor valor do coeficiente de atrito μ 2 para o par de superfícies inferiores, para o qual
60- O tensionador sustenta uma força trativa de 40k N no cabo. Os parafusos têm um diâmetro médio de 30m m e roscas quadradas com passo de 3.5m m . O coeficiente de atrito para as roscas lubrificadas
64- Resolva o Prob. 6/63 se a compressão na mola for de 200N . Todas as outras condições se mantêm iguais.
63- Calcule a força P necessária para mover a roda de 20k g . O coeficiente de atrito em A vale 0.25 e o de ambos os pares das superfícies das cunhas vale 0.30 . Além disso, a mola S está sob compress