Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 55
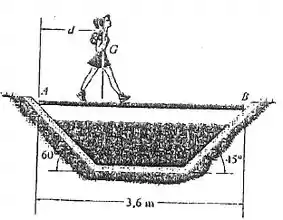
Se a garota com estiver na posição , determine o coeficiente mínimo de atrito estático nos pontos de contato e de modo que a tábua não deslize. Despreze o peso da tábua.
Passo 1
O problema pede que descubra o menor coeficiente de atrito estático para que a tábua fique parada, sem deslizar, ou seja em equilibrio.
Beleza, a gente vai começar fazendo um diagraminha de corpo livre com o peso da garota:
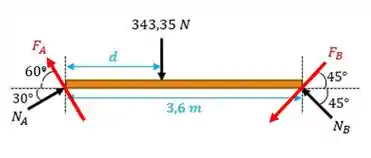
Vamos assumir que a tabua está na eminência de rotacionar no sentido anti-horário. Isso causa então que as forças de atrito sejam em sentidos opostos em relação ao eixo , e ambas tentem parar a rotação.
As forças de atrito são paralelas às superfícies inclinadas. E as forças de reação ficam normais a essas forças de atrito.
A forças de atrito que estão de vermelho são:
Isso porque estamos considerando a eminência de deslocamento.
Passo 2
Agora, a gente pode calcular as forças reação ( e ) usando os momentos.
Primeiro usando como eixo de relação e considerando o sentido anti-horário como positivo.
Agora usando :
Passo 3
Bom, infelizmente a gente ainda não pode econtrar a o que a gente quer porque ainda tem três variaveis e só duas equações, então vamos olhar o somatório das forças no eixo horizontal:
Ai substituimos:
Calma, tá quase acabando, agora a gente só precisa resolver isso, encontramos:
Isso vira uma equação do segundo grau, aí a gente resolve e escolhe a solução positiva
Ficou um pouco diferente do gabarito, mas estamos certinhos.