Calcule a distância medida desde a base até o centroide do volume do cone circular truncado.
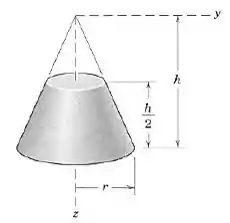
Passo 1
Sabendo que a equação para encontrar o centroide é dado por:
Dessa maneira, vamos primeiro encontrar o volume do problema.
Passo 2
Mas antes vamos escolher um elemento de volume, para assim podermos integrar, com isso:
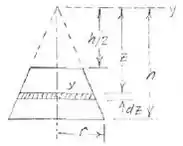
Pronto! Escolhido o elemento de volume vamos integrar ele em relação a z e temos o nosso volume.
Agora precisamos deixar em função de z para podermos integrar. O problema nos informa que o cone é circular, dessa maneira se olhamos por debaixo do cone, veremos que a área da base será:
Logo o volume é dado por:
Onde a função que descreve a geratriz é linear e dada por:
Com isso,
Passo 3
Tendo a função que descreve o nosso problema fica mais fácil de integrar, atente que a região de integração está entre . Dessa maneira:
Agora basta resolvermos essa integral que teremos nosso volume, sendo assim:
Passo 4
Ante de aplicar a equação para achar o centroide na coordenada x, vamos resolver a integral:
Depois é só dividir pelo volume que teremos o ponto. Com isso,
Logo,
Pronto! Só substituir na equação, se tiver alguma dificuldade na resolução das integrais recomendo que revise este assunto de integrais em cálculo que encontra na própria plataforma. Agora vamos substituir:
Passo 5
Calma ainda não acabou! Atente que o problema quer , que é da base até o centroide. Sendo assim: