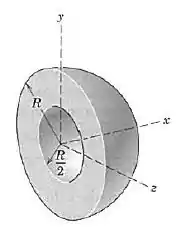
Determine a coordenada x do centro de massa do hemisfério homogêneo, que teve removida a região hemisférica menor.

Mas antes vamos escolher um elemento de volume, para assim podermos integrar. Atente que o volume que queremos é a do hemisfério menos a parte removida. Com isso:

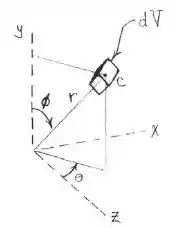
Pronto! Escolhido o elemento de volume, temos que integrar ele com relação a algo. Observe que estamos nos tratando de uma esfera, ou seja, podemos utilizar das coordenadas esféricas para acharmos o volume. Sabendo que, o volume em coordenadas esféricas é dado por:

Note também, que o , mostrado no desenho acima, varia de 0 a , assim como o , também varia de 0 a . Para completar o hemisfério. Já o raio, como é da parte que foi removida varia apenas de a .

Tendo a função que descreve o nosso problema fica mais fácil de integrar, dessa maneira o volume é dado por:

Não se assuste pela integral! Vamos resolvê-la em parte, de dentro para fora. Assim, resolvendo a de dentro temos:

Logo, o volume é:

Ante de aplicar a equação para achar o centroide na coordenada x, vamos resolver a integral:

Depois é só dividir pelo volume que teremos o ponto. Sabendo que em coordenadas esféricas o x é dado por:

Temos:

Simplificando:

Resolvendo-a do mesmo modo que resolvemos a anterior, teremos:

Pronto! Só substituir na equação, se tiver alguma dificuldade na resolução das integrais recomendo que revise o assunto de integrais triplas e coordenadas esféricas que encontra na própria plataforma. Agora vamos substituir: