Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 17

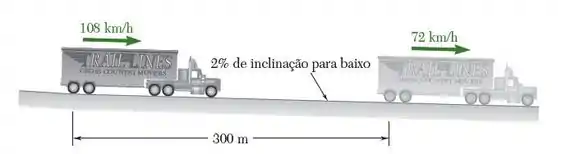
Um caminhão-baú entra em um declive com 2 % de inclinação deslocando-se a 108   km/h e deve reduzir para 72 km/h em 300 m. O cavalo mecânico tem uma massa de 1.800 kg e o baú, 5.400 kg. Determine (a) a força média de frenagem que deve ser aplicada, (b) a força média exercida no engate entre o cavalo mecânico e o baú se 70 % da força de frenagem é suportada pelo baú e 30 %   pelo cavalo mecânico.

Passo 1

Olá!! Tudo beleza? Neste problema devemos encontrar a força média de frenagem que deve ser aplicada para reduzir a velocidade do caminhão (item a) e a força média exercida no engate entre o cavalo mecânico e o baú se 70 % da força de frenagem é suportada pelo baú e 30 %   pelo cavalo mecânico (item b).

(a) Considerando o cavalo mecânico e o baú como corpo livre:

v 1 = 30   m / s

v 2 = 2 0   m / s

h = 0,02 ⋅ 300 = 6   m

d = 300   m

m = 1800 + 5400 = 7200   k g

W = m g = 7200 ⋅ 9,81 = 70632   N

Utilizando o princípio do trabalho e energia:

T 1 + U 1 → 2 = T 2

1 2 ⋅ m ⋅ v 1 2 + W h - F f r e i o d = 1 2 ⋅ m ⋅ v 2 2

Isolando F f r e i o

F f r e i o = 1 d 1 2 ⋅ m v 1 2 + W h - 1 2 ⋅ m v 2 2

F f r e i o = 1 300 1 2 ⋅ 7200 30 2 + 70632 ⋅ 6 - 1 2 ⋅ 7200 20 2

F f r e i o = 7412,6   N

(b)

Considerando apenas o baú como corpo livre, calcularemos a força no engate F C . Assumimos que o engate está tensionado (compressão).

Força de frenagem

F ' f r e i o = 0,7 ⋅ 7412,6 = 5188,82

m = 5400   k g

W = m g = 52974   N

Utilizando o princípio do trabalho e energia:

T 1 + U 1 → 2 = T 2

1 2 ⋅ m ⋅ v 1 2 + W h - F ' f r e i o d + F C d = 1 2 ⋅ m ⋅ v 2 2

Isolando F C

F C = F ' f r e i o - 1 d 1 2 ⋅ m v 1 2 + W h - 1 2 ⋅ m v 2 2

F C = 5188,82 - 1 300 1 2 ⋅ 5400 30 2 + 52974 ⋅ 6 - 1 2 ⋅ 5400 20 2

F C = - 3706,8   N

F C = 3706,8   N   ( c o m p r e s s ã o )

Resposta

(a) 7412,6   N

(b) 3706,8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros, e parte do topo da estrutura A com uma velocidade Va = 3 m/s. Determine a altura mínima h da estrutura de maneira que o ca
O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros. Se ele é solto do repouso no topo da estrutura A, determine a altura mínima h da estrutura de maneira que o carrinho dê a
O anel de 2,5 kg é solto do repouso em A e desloca-se ao longo da guia sem atrito. Determine a velocidade do anel quando ele bate no apoio B. A mola tem um comprimento não deformado de 0,15m.
O anel de 2kg é submetido a uma velocidade para baixo de 4m/s quando está em A. Se a mola tem um comprimento não deformado de 1m e uma rigidez k=30N/m, determina a velocidade do anel em s=1m
O anel C de 4kg tem uma velocidade v A = 2 m/s quando está em A. Se a barra-guia é lisa, determine a velocidade do anel quando ele está em B. A mola tem um comprimento não deformado l a = 0,2 m.