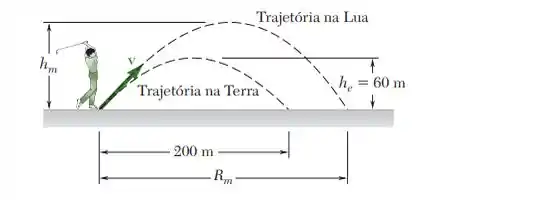
Uma bola de golfe golpeada na terra alcança uma altura máxima de 60 m e atinge o chão uma distância de 200 m. A que distância a mesma bola de golfe se desloca na Lua se a intensidade e direção de sua velocidade forem as mesmas que ela teria na Terra imediatamente depois de bola foi atingida? Considere que a bola é atingida e aterrissa com a mesma elevação em ambos os casos e que o efeito da atmosfera na Terra é negligenciado, de modo que a trajetória em ambos os casos é uma parábola. A aceleração da gravidade na Lua é 0,165 vezes daquela da Terra.

A sacada desta questão está na identificação do ponto 2 (ponto final) para utilizarmos o princípio do trabalho e energia. No início sabemos que, em ambas as trajetórias, a energia cinética é exatamente a mesma e é igual a:

Agora, até que ponto iremos analisar? Tem que ser algum ponto que nós conhecemos a relação de velocidade ou de altura!

E aqui está a sacada! Temos que analisar em relação ao ponto mais alto de cada trajetória. É necessário utilizar este ponto pois aqui conhecemos a velocidade do corpo. Em ambos a velocidade é , isto é, apenas a componente horizontal da velocidade .

Portanto, a energia cinética será:

E agora basta calcularmos o trabalho realizado pela força peso em cada trajetória. Para a Lua ela será:

E para a trajetória na Terra ela será:

Agora basta aplicarmos o princípio do trabalho e energia para cada um dos casos. Começando pela trajetória na Terra, temos:

Já para a trajetória da Lua, temos:

Agora, basta compararmos as duas relações. Com isto, temos:

Como e , então, será:

E assim finalizamos a questão.