Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 33
Um pistão de massa e seção transversal de área está em equilíbrio sob a pressão no centro de um cilindro fechado em ambas as extremidades. Admitindo que o cilindro seja empurrado para a esquerda a uma distância e liberado, e sabendo que a pressão em cada lado do pistão varia inversamente com o volume, determine a velocidade do pistão quando ele alcançar novamente o centro do cilindro. Despreze o atrito entre o pistão e o cilindro e expresse sua resposta em termos de , , e
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão!
Mas, não é por isto que não devemos identificar as forças do nosso problema e construir um diagrama de corpo livre. Portanto, este é o nosso primeiro passo (e até o mais importante!).
Então, fazendo o diagrama de corpo livre, temos,
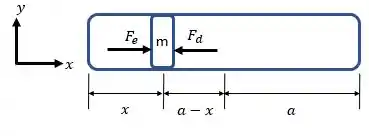
Passo 2
Antes de determinarmos a velocidade quando o pistão alcança o centro do cilindro, precisamos determinar as expressões para as forças a esquerda e a direita do cilindro, e respectivamente.
Como a força é o resultado da pressão vezes a área da seção transversal, temos:
E como as pressões e variam inversamente com o volume, isto é,
Temos então:
Passo 3
Agora temos todas as informações necessárias para aplicarmos o método que vemos aplicando nas questões anteriores, o princípio do trabalho e energia. Para o ponto inicial, em , o pistão está em repouso .
Queremos determinar qual a velocidade quando o pistão atingir a marca . Escrevendo a equação da energia cinética para ambos os pontos, temos:
Já o trabalho das forças e será:
Aplicando o princípio de trabalho e energia, temos:
E assim finalizamos a questão!