Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 116
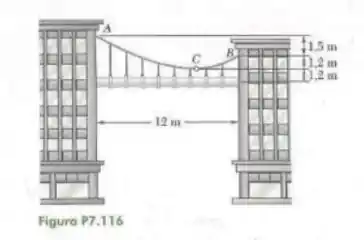
Um cano de vapor pesando que passa entre dois prédios, distanciados entre si, é sustentado por um sistema de cabos tal como mostra a figura. Considerando que o peso do cabo é equivalente a um carregamento uniformemente distribuído de , determine (a) a localização do ponto mais baixo no cabo, (b) a tração máxima no cabo.
Passo 1
Bom galera, vamos começar esboçando o cabo pra facilitar pra gente:
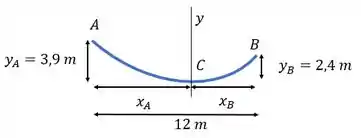
Logo:
Passo 2
Show de bola, agora a gente pode usar a equação :
Primeiro no ponto ?
Já no ponto :
Dividimos uma equação pela outra e ficamos com:
Resolvendo essa equação temos:
Passo 3
Por fim, vamos encontrar a tração máxima, primeiro sabemos que:
Assim:
E usamos a equação de novo para encontrar :
Resolvendo, encontramos:
Então, só falta Pitágoras pra terminar:
Resposta
Exercícios de Livros Relacionados
Um contrapeso D é fixado a um cabo que passa por uma pequena roldana em A é preso no suporte em B . Sabendo L = 13,5m e h = 4,5m , determine (a) o comprimento do cabo de A até B , (b) o peso por unida
Um fio de 20m de comprimento, que tem massa por unidade de comrpimento igual a 0,2k g / m está preso a um apoio fixo em A e a um colar em B . Desprezando o efeito do atrito, determine (a) a força P pa
Usando a propriedade indicada no Problema 7.124 , determine a curva assumida por um cabo de vão L e flecha h que sustenta uma carga distribuida w = w 0 cos ( π x / L ) , onde x é medido a partir do
Utilizando a propriedade estabelecida no problema 7.119 , resolva o problema indicado, resolvendo primeiro o problema de viga correspondente. Problema 7 . 100 a .
Utilizando a propriedade estabelecida no problema 7.119 , resolva o problema indicado, resolvendo primeiro o problema de viga correspondente. Problema 7.9 9 a .