Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 99

O corpo composto na figura é formado pela remoção de um semielipsoide de revolução de semieixo maior h e semieixo menor a / 2 a partir de um hemisfério de raio a . Determine (a) a coordenada y do centroide quando h = a / 2 , (b) a razao h / a para a qual y = - 0,4 a .

Passo 1

Bom galera, o problema quer que a gente encontre o centroide y - do corpo da figura, que pode ser encontrada com essa fórmula básica do centroide:

y - = y - V V

Passo 2

Show de bola, nós então montamos uma tabelinha simples com os volumes e os y - de cada solido que a gente conseguir separar pra facilitar, esse y - a gente encontrar lá no final do livro, então bora:

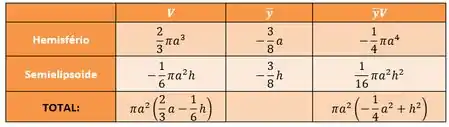
Passo 3

Então, a gente aplica aquela formula básica:

y - = y - V V

→ y - = π a 2 - 1 4 a 2 + h 2 π a 2 2 3 a - 1 6 h

→ y - = - 1 4 a 2 + h 2 2 3 a - 1 6 h

Passo 4

Por fim, a encontra o centroide y - quando h = a / 2 :

y - = - 1 4 a 2 + a 2 2 2 3 a - 1 6 a 2

→ y - = - 45 112 a = - 0,402 a

E a razão h a para y - = 0,4 a .

y - = 0,4 a = - 1 4 a 2 + a 2 2 2 3 a - 1 6 a 2

Simplificando e isolando, encontraremos que:

h a = 2 3

Resposta

y - = - 0,402 a

h a = 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y ¯ da área sombreada.
Localize o centroide y ¯ da área.
Localize o centroide x ¯ da área.
Localize o centroide y ¯ da área sombreada.
Localize o centroide y ¯ da área sombreada.