Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 27
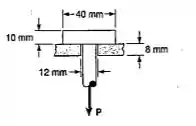
A carga P está aplicada na barra cilíndrica de aço, como indicado, e apoia-se numa placa de alumínio com furo de 12mm de diâmetro, feito por uma broca. Sabendo-se que a máxima tensão de cisalhamento é de 180MPa para o aço e 70MPa para o alumínio, determine a maior carga que pode ser aplicada à barra de aço.
Passo 1
Primeiro vamos entender o problema, e para isso precisamos olhar os pontos possíveis que possam ocorrer cisalhamento. O cisalhamento acontece em áreas paralelas à força.
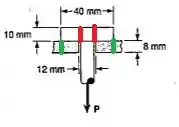
A área de vermelho é referente ao aço, e a verde é referente ao alumínio. No movimento para baixo, a barra pode fazer um furo na placa circular de aço ou essa placa circular pode furar o alumínio. Olhando de cima a gente pode ver melhor essas áreas, se liga:
As duas áreas são circulares sendo a maior o aço furando o alumínio e a menor a barra de aço furando a placa.
Passo 2
Vamos então calcular os pesos para cada caso. Para o aço a gente tem:
A espessura da placa de aço que é .
O diâmetro da barra de aço que vai causar o furo
Se liga aqui, a área que nos interessa é paralela à força então é a área lateral do cilindro que é o furo.
Usando a equação da tensão cisalhante a gente tem:
Passo 3
Para o alumínio:
A espessura da placa de alumínio que é .
O diâmetro da placa cilindríca de aço que vai causar o furo
Se liga aqui, a área que nos interessa é paralela à força então é a área lateral do cilindro.
Usando a equação da tensão cisalhante a gente tem:
Como o peso do aço foi o menor entre os dois, pegamos ele.