As hastes de ligação e são ambas de aço () e são de de largura por de espessura. Determinar: (a) a força em cada haste, quando uma força de é aplicada à barra rígida , como indicado: (b) a correspondente deflexão no ponto .
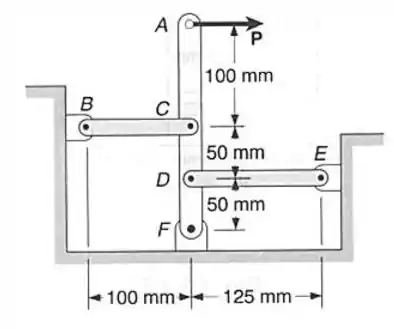
Passo 1
O problema pede as forças em cada haste, que não podem ser calculadas apenas pelas equações de equilíbrio, por se tratar de um problema hiperestático (mais variáveis que equações). Além das forças o problema pede a deflexão do ponto .
Logo, vamos ter que utilizar, além das condições de equilíbrio, a equação da deflexão. Isso para achar as forças e, posteriormente, achar a deflexão de .
Passo 2
Vamos fazer o diagrama de corpo livre da barra
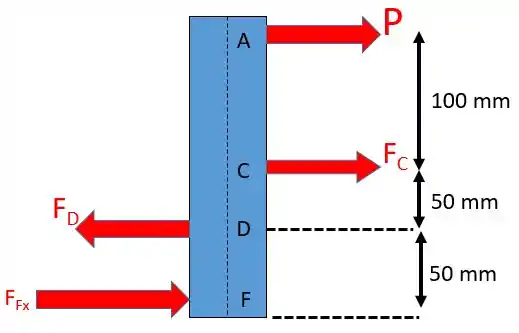
Existem algumas forças na vertical, porém como não fazem diferença para e resolução do problema serão desconsideradas.
De modo a eliminar a força da jogada iremos utilizar apenas a equação do momento com relação ao ponto .
Considerando o sentido horário positivo
Simplificando por 50
Para resolver o problema vamos ter de achar outras equações, correto? Mas nenhuma daquelas de equilíbrio estático vai nos ajudar mais, o que precisamos é achar a deflexão da barra.
Passo 3
Vamos calcular a deflexão da barra.
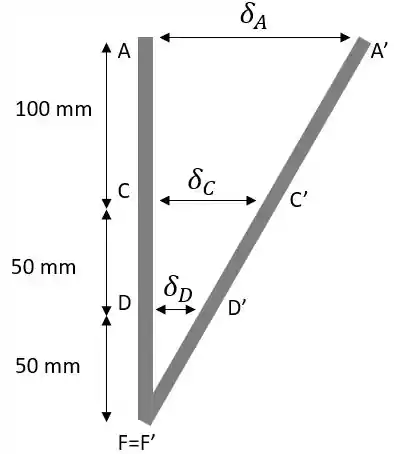
As deflexões dos pontos e vão ser as seguintes, lembrando que a equação é dada por:
Como o ponto muda de posição por causa da deflexão da barra , teremos:
Onde a área é igual a , assim
Da mesma forma para
Onde a área é igual a , assim
Agora temos as duas deflexões em função das forças.
Aí o PULO DO GATO é associar essas deflexões com a geometria. Vamos fazer isso no próximo passo.
Passo 4
Olha a geometria da figura
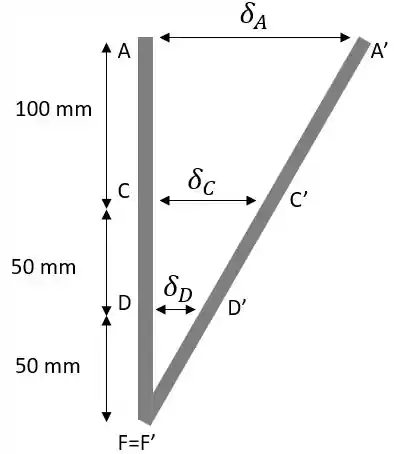
A gente pode ver que os triângulos e são semelhantes. Assim podemos fazer a seguinte relação:
Multiplicando cruzado
Simplificando
Agora se lembra das equações que a gente já tem? São essas aqui ó!
Então a gente tem 4 equações e 4 incógnitas, UHULLL!!!!
Passo 5
Agora vamos resolver esse sisteminha né?
Como a gente quer primeira as forças vamos substituir as deflexões:
De
Vamos ter
Agora vamos substituir isso em
Obtendo
Substituindo em
Obtemos
Passo 6
Agora, para achar a deflexão em a gente tem que voltar lá na geometria da figura. Isso porque o não pode ser calculado diretamente a partir da equação da deflexão, porque não existe uma haste ali!? Ta ligado!?
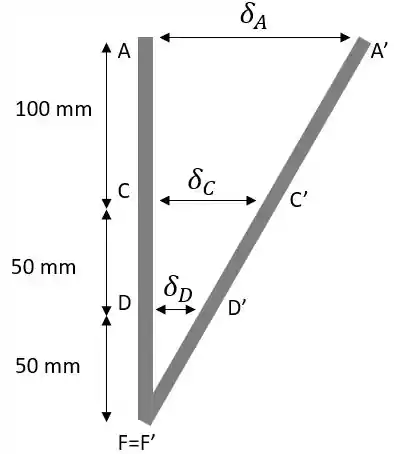
Pela geometria e pela semelhança vamos ter que
Logo
E é fácil achar através da força
Importante aqui que a força deve estar em para acharmos a deflexão em
Então
Resposta
a)
b)