Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 31

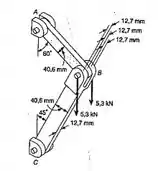
Para a montagem e o carregamento do Prob. 1.16, determine: (a) a tensão de cisalhamento média no pino A;(b) a tensão de esmagamento em A, na barra AB.

Dados: diâmetro do pino = 15,2mm

Passo 1

O item (a) pede a tensão cisalhante no pino A. Primeiro precisamos calcular os esforços na seção do pino. Para isso vamos desenhar um esquema mais simplificado, dessa forma:

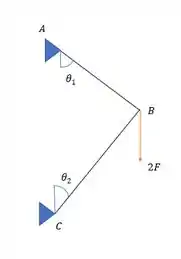
Onde 2F é 2 × 5,3 = 10,6 K N , θ 1 = 60 ° e θ 2 = 45 ° .

Vamos fazer o somatório das forças no nó B, e encontrar uma relação entre as forças, um macete aqui para pensar no sentido das forças é observar que combinações podem levar ao equilíbrio. Na vertical a gente precisa combater a força 2F mas na horizontal as forças precisam ser iguais.

∑ F H = F A B s e n θ 1 - F B C s e n θ 2 = 0

F B C = F A B s e n θ 1 s e n θ 2   ( 1 )

∑ F v = F A B c o s θ 1 + F B C c o s θ 2 = 2 F   ( 2 )

Substituindo os valores na equação 1, temos:

F B C = 1,22 F A B

Usando esse valor na equação 2 e substituindo os outros valores:

F A B c o s 60 + 1,22 × F A B c o s 45 = 2 F

1,362 F A B = 2 F

F A B = 10,6 1,362 = 7,8 K N

Passo 2

Agora que temos o esforço, basta dividirmos pela área do pino que sofre cisalhamento.

O pino tem duas áreas que são paralelas e resistem ao esforço.

A p i n o = 2 A = 2 π d 2 4 = 363 m m ²

E enfim:

τ = F A B A p i n o

Passando a força de KN para N, temos:

τ = 7,8 × 10 3 363 = 21,5 M P a

Passo 3

Para o item b, a gente precisa olhar para a seção transversal da barra por onde o pino passa. Vamos desenha-la para entender legal.

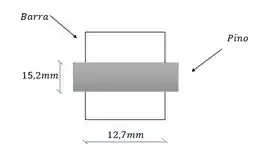
A área na barra no ponto A que sofre esmagamento, é a área por onde passa o pino.

A = 12,7 × 15,2 = 193,04 m m ²

A tensão de esmagamento em A é dada então por:

σ = F A B A = 7,8 × 10 3 193,04 = 40,41 M P a  

Resposta

  1. τ = 48,72 M P a
  2. τ = 53,6 M p a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as barras do P r o b .2 . 49 , vamos considerar que depois de ser perfeitamente ajustada cada uma das porcas A e C é afrouxada de meia volta. A temperatura de ambas as barras é então diminuída de
Para as barras do P r o b .2.63 , determinar:A temperatura á qual a tensão na barra AB deve ser de - 138M P a ;A correspondente deformação na barra AB.
Um medidor de deformação localizado em C na superfície do osso AB indica que a tensão normal média no osso é de 3,80 MPa quando o osso é submetido a duas forças de 1200 N, como mostra a figura. Supond
Duas hastes cilíndricas sólidas AB e BC são soldadas uma a outra em B e submetidas a um carregamento como mostrado na figura. Dados d1= 130 mm e d2= 250 mm, encontre a tensão normal média na seção cen
Duas barras cilíndricas de seção transversal cheia AB e BC são soldadas uma à outra em B e submetidas a um carregamento conforme mostra a figura. Sabendo que P = 10 kips, encontre a tensão normal médi