Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 51
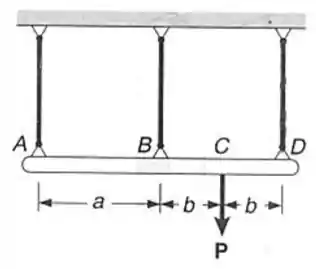
A barra rígida é suspensa por três cabos idênticos, como indicado. Sabendo-se que , determinar a tração em cada cabo, causada pela carga aplicada em .
Passo 1
Com a aplicação da carga haverá, além das forças nos cabos, uma deflexão na barra. A partir da equação de equilíbrio estático, da geometria e das equações de deflexão de cada cabo vamos conseguir achar as trações.
Passo 2
Vamos fazer, primeiramente, o diagrama de corpo livre da barra.
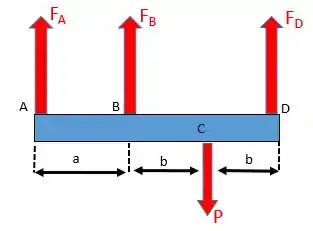
Aplicando a soma das forças em
Com as relações de equilíbrio estático vamos aplicar o momento em qualquer ponto, no caso o ponto
como
Simplificando por
Obtendo assim duas equações:
Passo 3
Agora vamos analisar a geometria, quando há a deflexão.
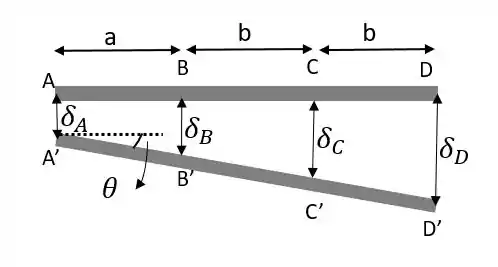
Os pontos foram mudados para as posições . Se traçarmos uma paralela (pontilhada) vamos observar que as deflexões serão dadas da seguinte forma:
Como
Passo 4
Agora vamos calcular cada deflexão:
Como os três cabos são idênticos, o único termo que irá mudar é o termo da força, logo:
E será obtido a partir da relação do passo 3.
Passo 5
Vamos juntas as equações do passo 4 com as do passo 5, assim vamos ter:
1)
Isolando as forças
2)
Isolando as forças
Agora substituímos na equação
Obtendo
Isolando o termo
Passo 6
Com isso vamos aplicar a outra equação também para descobrir
Como a gente já isolou o termo podemos substitui-lo agora
Multiplicando os dois lados por 10
Agora podemos substituir em
Obtendo duas novas equações
Subtraindo a primeira pela segunda
E finalmente vamos ter
Portanto temos as nossas trações