Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 109

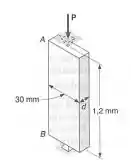
Uma carga centrada P deve ser suportada pela barra de aço AB. Sabendo-se que σ e = 250   M P a   e   E = 200   G P a ,   determinar a menor dimensão d da seção transversal que pode ser usada, quando : (a) P = 60   k N ; b P = 30 k N .

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine a menor dimensão d da seção transversal, então partiu :D

C c = 2 π 2 E σ γ = 2 π 2 200 × 10 9 250 = 125,66

L e = L = 1,4 m

A = 3 d d = 3 d 2

I = 1 12 3 d d 3 = 1 4 d 4

Temos a seguinte relação “diâmetro “

r = I A = d 12 = 0,288675 d

Passo 2

  1. P = 60 × 10 3 N                     A s s u m a L e r > C c

    2. P μ = π 2 E I 1,92 L e 2             I = 1,92 P μ L e 2 π 2 E = 1 4 d 4

    d 4 = 4 1,92 P L e 2 = 4 1,92 60 × 10 3 1 , 2 2 π 2 200 × 10 9 = 336,16 × 10 - 6 m 4

    d = 0,135   m     r = 0,067   m

    Passo 3

  2. P = 30 × 10 3 N                       A s s u m e L e r > C c

d 4 = 4 1,92 P L e 2 π 2 E = 4 1,92 30 × 10 3 1 , 2 2 π ² 200 × 10 9 = 1,68 × 10 - 7 m 4

d = 20,24 × 10 - 3 m             r = 10,12 × 10 - 3   m

L e r = 1 , 2 10,12 × 10 - 3 = 1 18,545 > 125,66      

  d = 20,24 × 10 - 3 m

Resposta

  1. 0,067   m
  2. 10,12 × 10 - 3   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma coluna uniforme, de 5,5m de comprimento efetivo, consiste de um tubo de aço, com a seção transversal mostrada. Usando o método da interação, determinar a carga admissível P, quando a excentricidad
Resolver o Prob. 11.118 usando o método da interação
Um poste de madeira de 220mm de diâmetro está livre em seu topo A e engastado em sua base B. Para o tipo de madeira usada E = 12G P A e a tensão admissível à compressão, paralela às fibras, é de 10 Mp
Uma carga centrada de 65kN é aplicada a um poste de 5m, que está livre em seu topo A e engastado em sua base B. Usando uma madeira para a qual E = 11 G P a e a tensão admissível à compressão, paralela
Resolver o Prob. 11.122, usando o método da tensão admissível