Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 128
A carga distribuída é suportada por duas colunas acopladas por pinos, cada uma com seção transversal circular maciça. Se AB for feita de alumínio e CD de aço, determine o diâmetro exigido para cada coluna, de modo que ambas estejam na iminência de sofrer flambagem ao mesmo tempo. ;
Passo 1
Oláaaa! Tá bem? Então, ele quer saber o diâmetro das colunas AB e CD para que elas estejam no limite de sofrer flambagem por causa do carregamento da viga.
Aí percebe que as forças axias nas colunas são as reações de apoio em relação ao carregamento na viga. Então a gente precisa descobrir essas reações de apoio.
Essa carga distribuída é equivalente a uma carga concentrada de valor igual a área do triângulo que a representa
Ela está a um terço da base do triângulo em . Temos essa situação:
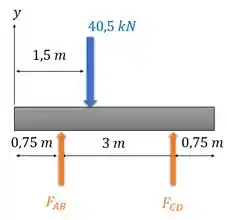
Passo 2
Vamos calcular o momento no ponto , considerando o sentido anti-horário positivo:
E agora o equilíbrio na direção vertical:
Passo 3
Beleza, a agora a gente precisa olhar para cada coluna separadamente. Queremos que a coluna (que é de alumínio) esteja na eminência de sofrer flambagem. Isso significa que a carga crítica dela vai ser igual ao esforço normal que ela sofre, ou seja,
E qual é a expressão da carga crítica? Essa aqui:
Como a coluna está presa por pinos nas extremidades, Temos , o comprimento da coluna é . E o momento de inércia é de uma seção circular:
Substituindo essas coisas e na expressão da carga crítica:
Isolando quem a gente quer, o :
Passo 4
A gente precisa confirmar que a coluna não entre em escoamento com essa dimensão e com . Então vamos calcular a tensão normal nela:
Como essa tensão é menor que a tensão admissível do alumínio que é de , a coluna está tranquila, e o nosso resultado é válido.
Passo 5
Vamos repetir o processo que fizemos para . Queremos que a coluna (que é de aço) esteja na eminência de sofrer flambagem. Isso significa que a carga crítica dela vai ser igual ao esforço normal que ela sofre, ou seja,
Como a coluna está presa por pinos nas extremidades, Temos , o comprimento da coluna é . E o momento de inércia é de uma seção circular:
Substituindo essas coisas e na expressão da carga crítica:
Isolando quem a gente quer, o :
Passo 6
A gente precisa confirmar que a coluna não entre em escoamento com essa dimensão e com . Então vamos calcular a tensão normal nela:
Como essa tensão é menor que a tensão admissível do aço que é de , a coluna está tranquila, e o nosso resultado é válido.