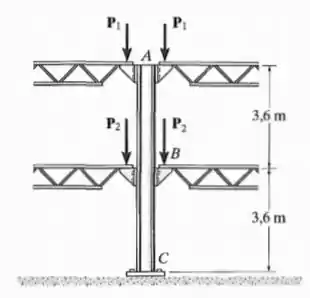
A coluna de aço é usada para suportar as cargas simétricas dos dois pisos de um edifício. Determine as cargas e se se mover para baixo e se mover para baixo quando as cargas forem aplicadas. A coluna tem área de seção transversal de .
Passo 1
E aí, meus camaradas tudo certo por aí? Prontos pra mais uma resolução?
Vamos lá, primeiro de tudo vamos deixar aqui anotado todos os dados fornecidos no exercício, além do módulo de elasticidade que é tabelado para o aço que estamos trabalhando que é aço , temos então
A gente colocou negativo essa mudança de altura dos pontos e porque eles descem.
Ele quer saber o valor de e , com base nessas deformações da coluna. Essas deformações acontecem porque essas forças causam compressão na coluna, e por isso a contraem.
Então, falou de alongamento (ou contração como nosso caso) e forças aplicadas, a gente pensa logo nessa fórmulinha do alongamento :
Onde é a força normal interna na haste, é o comprimento da nossa haste, é o módulo de elasticidade do material e é a seção transversal da coluna.
Só que temos que tomar um cuidado porque no meio da coluna temos forças aplicadas. Quando isso acontece, precisamos dividir nossa peça nesse ponto onde há força concentrada e usar essa fórmulinha para os dois pedaços que surgem separadamente.
Então vamos subdividir nossa barra em dois pedaços para a análise. Primeiramente usaremos a expressão do alongamento da parte e depois da parte . Isso vai nos dá duas equações que usam e . Logo teremos um sisteminha para resolver e achar elas. Bora!
Passo 2
Agora, meu cheiro, vamos observar o segmento . Precisamos saber a força normal interna nele, então vamos fazer uma seção nele:
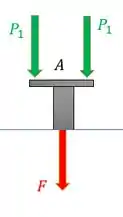
Colocamos a força saindo da seção porque esse é o sentido positivo da força normal, quando ela é força de tração. Pelo equilíbrio de forças da figura tiramos que a força normal nesse segmento é
Percebe que a nossa força ficou negativa, ou seja, ela na verdade está entrando na seção e vai ser uma força de compressão. E essa força causa uma contração no segmento.
Passo 3
Agora precisamos de , que é a contração do segmento .
O enunciado diz que o ponto desce . Mas percebe que isso não é a apenas a contração do segmento . Isso porque o segmento está sobre o segmento . Se é contraído, todo segmento desce.
Daí a gente tira que essa diminuição na altura do ponto tem dois motivos. O primeiro é a contração de , e o segundo é a diminuição de altura de , que é causada pela contração de , que vamos chamar de , que é igual . Então a gente pode escrever que
Substituindo os valores que a gente tem:
Esse alongamento é negativo porque isso é uma contração, tá bem? Aí agora a gente pode usar a fórmulinha do alongamento:
Substituindo os valores:
Isolando :
Passo 4
Bora dá uma respirada agora que a gente tá quase acabando. Como eu disse antes a gente vai trabalhar agora com o segmento . Queremos a força normal nesse segmento, então vamos fazer uma seção nele
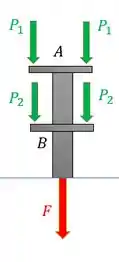
Pelo equiíbrio, temos que a força normal é de compressão e vale
E a contração desse segmento é o próprio , então
Aí a gente pode usar a expressão do alongamento:
Substituindo os valores:
Passo 5
Vamos isolar :
E substituir nosso valor de :
Pronto, finalmente acabamos essa questão vamos aos refrescos.
