Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 84

a) Para o carregamento axial mostrado, determine a variação em altura e a variação em volume do cilindro de latão mostrado na figura.

b) Resolvea parte (a) considerando que o carregamento seja hidrostático com σ x = σ y = σ z = - 70   M P a .

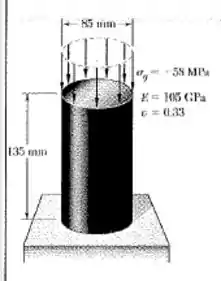
Passo 1

Para começar temos que h 0 = 135 m m .   Para facilitar nossas contas podemos reescrever como

h 0 = 0,135 m

Temos ainda que a área da seção circular nos vai ser dada por

A 0 = π 4 d 0 2 = π 4 85 2 = 5,6745 × 10 3   m m 2 = 5,6745 × 10 - 3   m 2

Passo 2

Para o cálculo do v 0 fazemos

v 0 = A 0 h 0

= 766,06 × 10 3   m m 2

= 766,06 × 10 - 6   m 3

Passo 3

Com isso tudo agora podemos entrar na resolução da questão propriamente dita. Vamos ter nesse caso que σ x = 0 ,   σ y = - 58 × 10 6 P a ,   σ z = 0 já qe o carregamento vem só de uma direção (eixo y).

ε Y nos será dado então por

ε y = 1 E - v σ x + σ y - v σ z = σ y E

= - 58 × 10 6 105 × 10 9 = - 552,38 × 10 - 6

Para a variação da altura fazemos

∆ h = h 0 ε y = 135   m m - 552,38 × 10 - 6 = - 0,0746   m m

Opa, encontramos então a variação da altura.

Passo 4

Para a variação do volume fazemos

e = 1 - 2 v   E σ x + σ Y + σ Z = 1 - 2 v ( σ y ) E

= 0,34 - 58 × 10 6 105 × 10 9 = - 187,81 × 10 - 6

Então encontramos o resultado procurado com a relação

∆ v = v 0 e

= 766,06 × 10 3   m m 3 - 187,81 × 10 - 6 = - 143,9

Passo 5

Para a letra (b) temos uma passo a passo muito similar, com exceção de que agora existe um carregamento também no eixo x e z.

σ x = σ y = σ z = - 70   M P a

Vamos começar calculando o ε y para calcularmos a variação da altura.

ε y = 1 E - v σ x + σ y - v σ z

= 1 105 × 10 9 - 0,33 - 70 + - 70 - 0,33 - 70 × 10 6

- 226,67 × 10 - 6

Teremos então a variação da altura como

∆ h = h 0 ε y = 135   m m - 226,67 × 10 - 6 = - 0,0306   m m

Passo 6

Para variação do volume faremos

e = 1 - 2 v   E σ x + σ Y + σ Z = 0,34 - 70 - 70 - 70 × 10 6 105 × 10 9 = - 680 × 10 - 6

Podemos então descobrir a variação do volume por meio de

∆ v = v 0 e

766,06 × 10 3   m m 3 - 680 × 10 - 6 = - 521   m m 3

Resposta

a ) ∆ h = - 0,0746   m m

∆ v = - 143,9   m m 3

b )   ∆ h = - 0,0306   m m

∆ v = - 521   m m 3  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força axial e cenrada, de intensidade P = 40k N , é aplicada à barra de aço mostrada. Determinar o máximo valor da tensão normal. (a) em A; (b) em B
A tensão normal admissível para o aço da barra mostrada vale 125 Mpa. Determinar a máxima força P admissível, axial e centrada, que pode ser aplicada a barra sabendo-se que d = 100 m m r = 15m m r = 2
Uma força axial é centrada, de intensidade P = 270k N é aplicada à barra de aço mostrada. Determine o máximo valor da tensão normal na barra, sabendo-se que: d = 120m m e r = 15m m d = 100m m e r = 25
Para o corpo de prova do Problema 2.86, determinar o máximo valor da tensão normal correspondente ao alongamento total de 0,75m m
A barra ABC consiste em duas porções cilíndricas AB e BC; ela é feita de um aço doce, que é assumido ser elastoplástico com E = 200 G P a e σ e = 250M P a . Uma força P é aplicada à barra e depois rem